14.2. Ортогональные полиномы и функции непрерывного типа

Перечислим некоторые из наиболее часто применяемых полиномов и кратко рассмотрим их свойства.

1. Полиномы Лежандра (первого рода), определяемые формулой

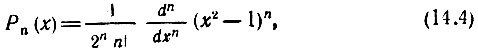
ортогональны с весом ρ(х) = 1 на интервале - 1 < х < 1. При целых n ≥ 0 полиномы Р_n(х) содержат конечное число членов.

Полиномы Лежандра низших степеней, графически представленные на рис. 14.1, определяются выражениями

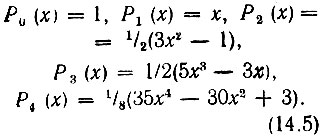
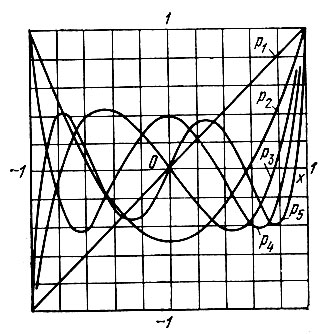
Рис. 14.1. График полиномов Лежандра

Квадрат нормы функции Р_n(х) в соответствии в формулой (14.4) равен [15, 16]

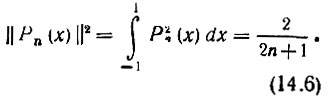
Выражение (2.9) для коэффициентов c_n принимает при этом форму

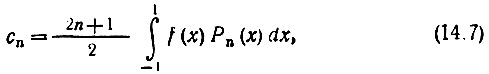
а ряд (2.8)

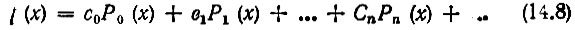
2. Полиномы Чебышева (первого рода) определяются как

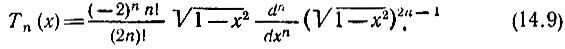
Полиномы Чебышева низших степеней

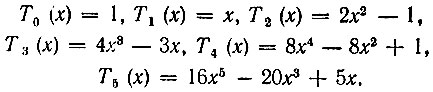
На рис. 14.2 представлены графики полиномов Т_n(х) на интервале -1 < х < 1, а на рис. 14.3 одного из них, в частности четвертого порядка, при 0 < |х| < 5/4. При |х| > 1 Т_n(х) стремится к бесконечности как 2^n-11 хⁿ.

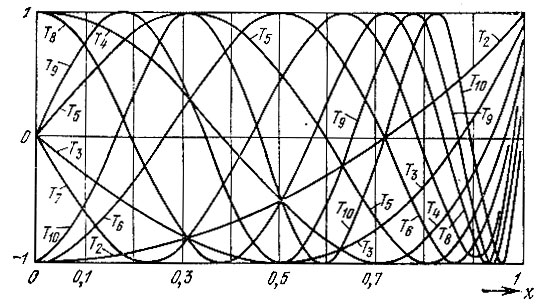
Рис. 14.2. Графики полиномов Чебышева

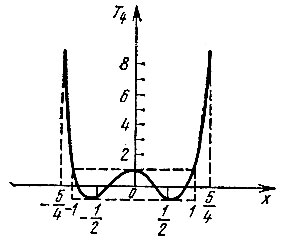
Рис. 14.3. Графики полиномов Чебышева четвертого порядка

Важной особенностью полиномов Чебышева является то, что из всех многочленов степени n со старшим коэффициентом, равным единице, они наименее уклоняются от нуля на отрезке -1 < х < 1. Благодаря этому свойству полиномы Чебышева обеспечивают наименьшую максимальную ошибку равномерной аппроксимации на интервале -1 < х < 1.

Полиномы Чебышева не ортогональны, но после умножения на 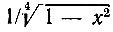они образуют ортогональную в интервале -1 < х < 1 систему функций 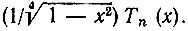Иными словами, полиномы Т_n(х) ортогональны с весом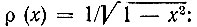

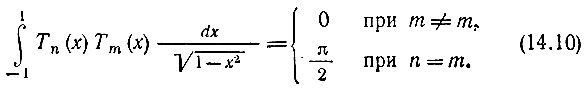
Кроме того, при m = n = 0

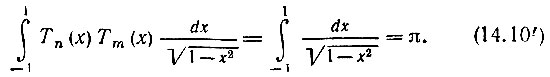
Таким образом, норма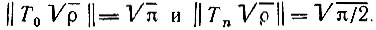

При разложении функции f(х) по полиномам Чебышева (с учетом Т₀(х) = 1) коэффициенты ряда

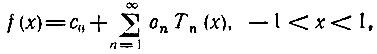
должны определяться в соответствии с (14.2) и (14.10), (14.10') следующими выражениями:

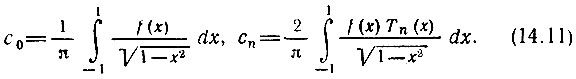
Поведение полиномов Чебышева в интервале -1 < х < 1 в сочетании с неограниченным возрастанием |Т_n(х)| при |х| > 1 делает эти полиномы очень эффективными для аппроксимации амплитудно-частотных характеристик различных фильтров. Этот вопрос рассматривается в гл. 15.

3. Полиномы Лагерра определяются формулой

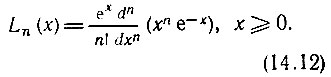
Первые четыре полинома:

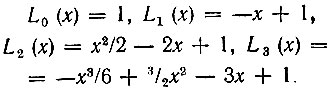
Полиномы Лагерра ортогональны на полуоси 0 < х < ∞ с весом ρ(х) = е^-х.

Так как полиномы Лагерра образуют систему расходящихся при х → ∞ функций, удобнее пользоваться функциями Лагерра

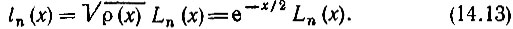
При этом функции Лагерра l_n(х) ортогональны с единичным весом. На рис. 14.4 приведены функции Лагерра при n = 1, 2, 5. Норма функции l_n(х)

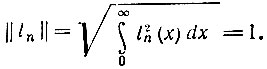
поэтому при разложении функции f(х) по функциям Лагерра коэффициенты ряда

должны определяться по формуле

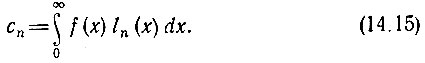
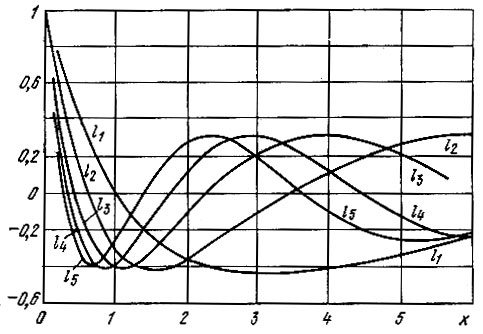
Рис. 14.4. Функции Лагерра

Функции Лагерра получили широкое распространение в измерительной технике и в многоканальных системах связи, что в значительной степени объясняется простотой их генерирования. Дело в том, что функция l_n(t) по форме совпадает с импульсной характеристикой физической цепи, составленной из каскадного соединения простых звеньев (рис. 14.5). Для определения передаточной функции требуемой цепи применим преобразование Лапласа к функции Лагерра (14.13), предварительно заменив в (14.12), (14.13) переменную х новой переменной х = αt:

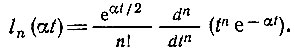
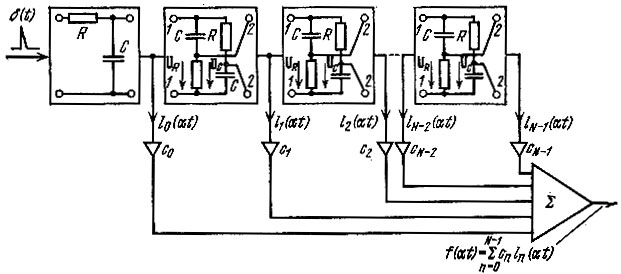
Рис. 14.5. Генератор функций Лагерра

Функции времени 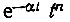соответствует изображение 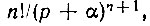а n - кратному дифференцированию - умножение изображения на рⁿ. Учитывая также, что умножение на e^αt/2 дает сдвиг на p-плоскости на величину -α/2, приходим к следующему изображению для функции Лагерра:

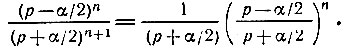
Передаточная функция первого звена 1/(р + α/2) реализуется интегрирующей RС-цепью, отвечающей условию RC = 2/α. Передаточная функция (р - α/2)/(р + α/2) соответствует мостовой схеме при RC = 2/α.

Действительно, непосредственно из мостовой схемы одного звена (рис. 14.5) следуют соотношения

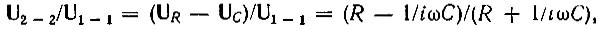
откуда

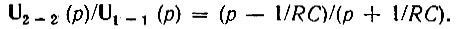
При возбуждении цепи (рис. 14.5) дельта-функцией колебание на выходе первого звена будет 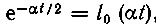а на выходах последующих звеньев соответственно l₁(αt), l₂(αt) и т. д.

Взвешенное суммирование всех этих колебаний дает на выходе сумматора колебание

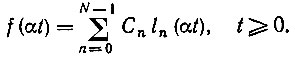
4. Полиномы Эрмита определяются формулой

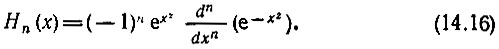
Первые пять полиномов Эрмита:

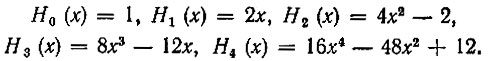
Графики этих полиномов представлены на рис. 14.6.

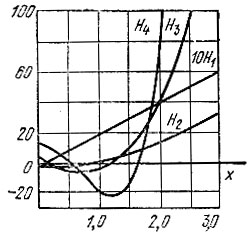
Рис. 14.6. Графики полиномов Эрмита

Полиномы Эрмита ортогональны с весом 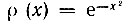на всей оси -∞ < х < ∞, так что

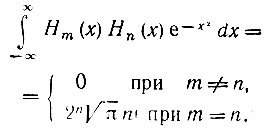
Таким образом, норма функции 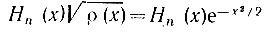равна

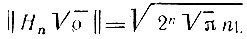
Для перехода к ортонормированной системе полиномов Эрмита вводят функцию

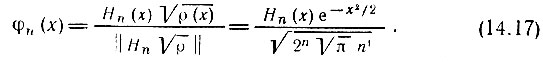
При этом разложение функции f(х) по нормированным функциям Эрмита записывается в форме

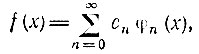
где

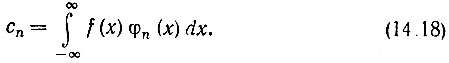
Графики нормированных функций φ_n(х) приведены на рис. 14.7. Из сделанного перечисления видно, что ортогональные системы функций можно разбить на два класса: 1) системы, определенные на

конечном интервале (полиномы Лежандра и Чебышева); 2) системы, определенные на бесконечном интервале, представляющем собой полуось 0 < х < ∞ (полиномы Лагерра) или всю ось -∞ < х < ∞ (полиномы Эрмита). Для аппроксимации процессов и характеристик, определенных на конечном интервале, естественно применять ортогональные системы первого вида. Для функций f(х), заданных в бесконечном интервале, целесообразно применять системы второго вида.

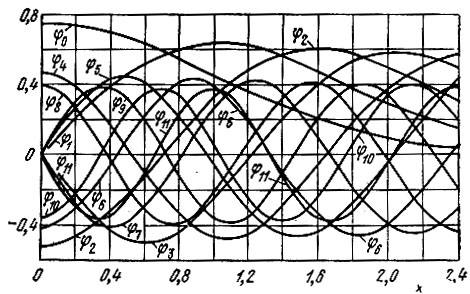
Рис. 14.7. Графики нормированных функций Эрмита

При выборе полиномов важное значение имеет вид весовой функции ρ(x), соответствующей тому или иному виду полинома. Этот выбор должен быть тесно увязан с характером аппроксимируемой функции f(x): весовая функция ρ(х) должна достигать максимума на участке, где требуется наилучшая аппроксимация. При этом появляется возможность уменьшения числа членов ряда при заданной допустимой ошибке аппроксимации. Выбором весовой функции можно также осуществить аппроксимацию процессов конечной длительности полиномами второго вида (определенными на бесконечном отрезке). Для этого необходимо, чтобы эффективная длительность весовой функции была близка к длительности аппроксимируемого сигнала.