14.3. Примеры применения непрерывных функций

Для упрощения вычислений и для большей наглядности функции, подлежащие аппроксимации, будем задавать в аналитической форме. Следует при этом иметь в виду что в действительных условиях часто приходится аппроксимировать функции, получаемые в результате эксперимента и заданные в виде таблиц, графиков, осциллограмм и т. д.

Рассмотрим разложение полуволнового косинусоидального импульса (рис. 14.8) по различным ортогональным полиномам. Представленная на рис. 14.8 функция

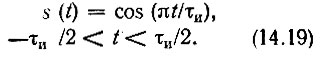
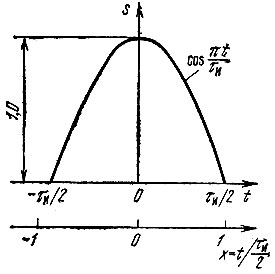
Рис. 14.8. Полуволновой косинусоидальный импульс

Переходя к безразмерному времени 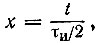получаем

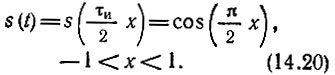
Так как функция 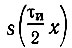задана в конечном интервале (-1, 1), то целесообразно рассмотреть разложение этой функции по полиномам Лежандра и Чебышева. Предварительно, однако, приведем разложение функции s(t) по тригонометрическим функциям с периодом Т, равным длительности импульса τ_и, чему соответствует безразмерный период х_T = 2 (рис. 14.8).

Так как 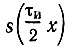четная функция, получаем косинусоидальный ряд

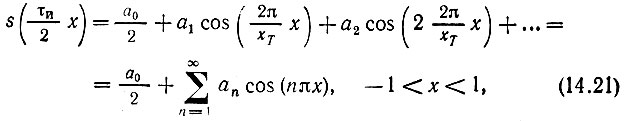
коэффициенты которого в соответствии с (2.32)

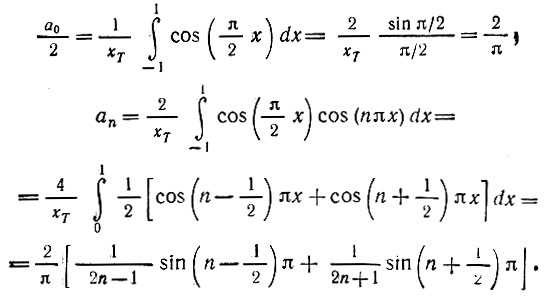
Прямым вычислением находим

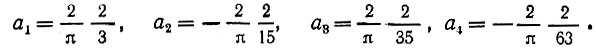
Спектр функции 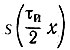по тригонометрическим базисным функциям cos nπх показан на рис. 14.9, а, а графики отдельных слагаемых ряда (14.21) - на рис. 14.9, б.

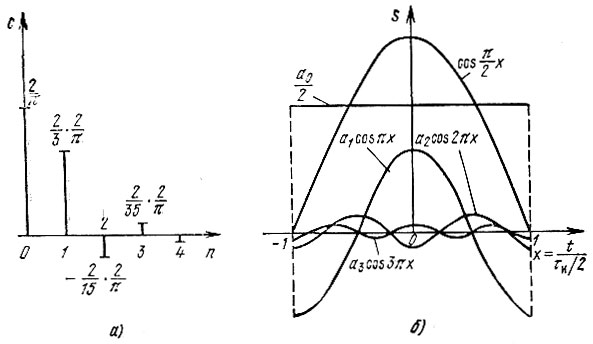
Рис. 14.9. Спектр полуволнового косинусоидального импульса в базисе тригонометрических функций (а) и первые четыре слагаемых ряда Фурье (б)

При использовании полиномов Лежандра коэффициенты ряда (14.8) в соответствии с (14.7) будут

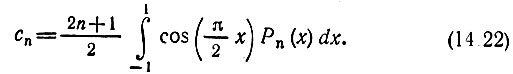
Таким образом,

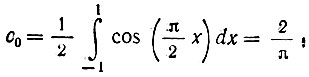
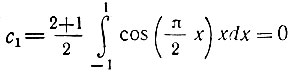
(интеграл от нечетной функции);

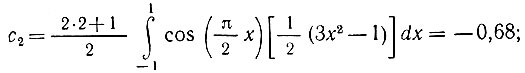
с₃ = 0 (интеграл от нечетной функции);

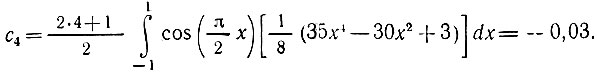
Итак,

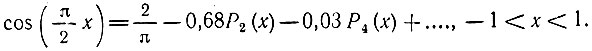
С помощью таблиц полиномов Лежандра [15] можно построить график 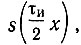показанный на рис. 14.10. Практически достаточно двух-трех членов ряда для удовлетворительной аппроксимации функции

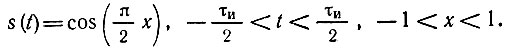
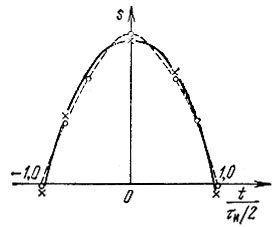
Рис. 14.10. Аппроксимация полуволнового косинусоидального импульса первыми тремя полиномами Лежандра (сплошная линия) и Чебышева (штриховая)

Рассмотрим теперь разложение этой функции по полиномам Чебышева. Вычисление коэффициентов с_n для функции 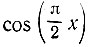облегчается наличием формулы (см. [16], формула (7.355.2))

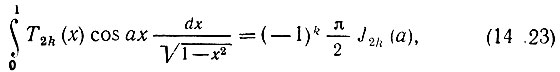
в которой J_2k(а) - функция Бесселя. При этом формулы (14.11) принимают вид

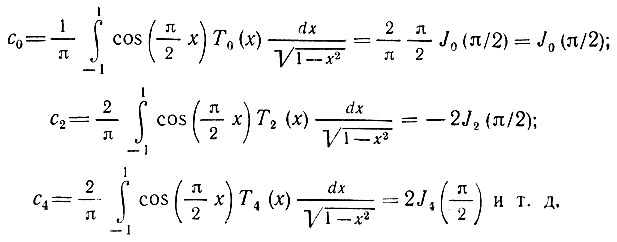
Функции J₀(m) и J₁(m) табулированы [15], а при более высоких порядках n = 2, 3, 4, ... можно использовать соотношения

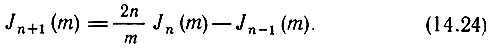
При аргументе m = а = π/2 по таблицам находим J₀(π/2) = 0,473 и J₁(π/2) = 0,566. Тогда

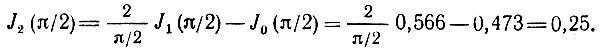
Далее,

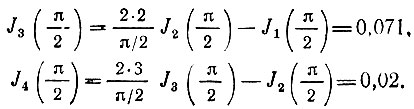
Таким образом, с₀ = 0,473; с₂ = -0,5; с₄ = 0,04 и т. д. Окончательно

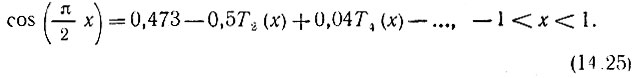
Сумма трех первых членов ряда представлена на рис. 14.10 (штриховая линия). Видно, что для удовлетворительной аппроксимации функции 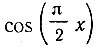достаточно трех членов ряда.

Из сопоставления трех аппроксимаций функции 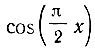видно, что тригонометрический ряд Фурье требует суммирования большего числа членов разложения, нежели полином Лежандра или Чебышева. Из двух последних разложений несколько меньшую ошибку в точке x = 0 (при суммировании всего лишь двух членов ряда) дает разложение по полиномам Лежандра. Однако в точке x = 1 приближение к точному значению (нулю) лучше по Чебышеву, чем по Лежандру. Это объясняется тем, что весовая функция 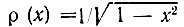возрастает с приближением х к единице.

Из приведенного сопоставления не следует делать вывод, что представление функций в форме тригонометрических рядов во всех случаях менее предпочтительно, чем разложение в ряд по полиномам.