14.4. Определение функций Уолша

Функции Уолша и Радемахера, известные с 1922 г., были надолго преданы забвению. Интерес к этим функциям и широкое их распространение связаны с развитием вычислительной техники.

Существуют различные способы определения функций Уолша. Рассмотрим способ, основанный на взаимосвязи функций Уолша с функциями Радемахера. Последние, в свою очередь, получаются из синусоидальных функций с помощью соотношения

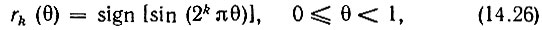
где аргумент θ = t/T₀ есть безразмерное время, т. е. время, нормированное к произвольному интервалу T₀, а целое положительное число k - порядок функции. Символом sign (сигнум-функция) обозначается функция

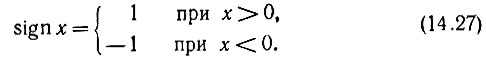
В соответствии с (14.26) и (14.27) функции Радемахера, принимающие одно из двух значений ±1, имеют вид меандра. Первые четыре функции Радемахера представлены на рис. 14.11.

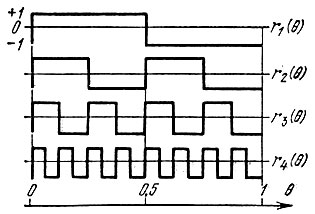
Рис. 14.11. Первые четыре функции Радемахера

Функции Радемахера ортонормированы (см. § 2.2) с единичной весовой функцией на интервале 0 ≤ θ < 1. Действительно, для любых двух функций r_m(θ), r_n(θ) имеют место соотношения

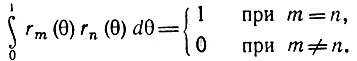
Все функции Радемахера являются нечетными относительно середины интервала определения и, следовательно, не могут быть использованы для аппроксимации сигналов s(θ), четных относительно момента θ = 1/2. Иными словами, система функций Радемахера - неполная (см. § 2.2).

Функции Уолша, образующие полную ортонормированную систему, можно сформировать, образуя произведения степеней соответствующих функций Радемахера. Первые восемь функций Уолша представлены на рис. 14.12. Сопоставление этих функций с функциями Радемахера (рис. 14.11) позволяет составить очевидные, по крайней мере для первых четырех функций Уолша, соотношения

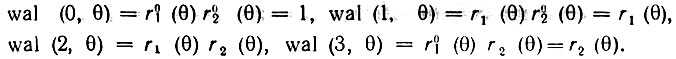
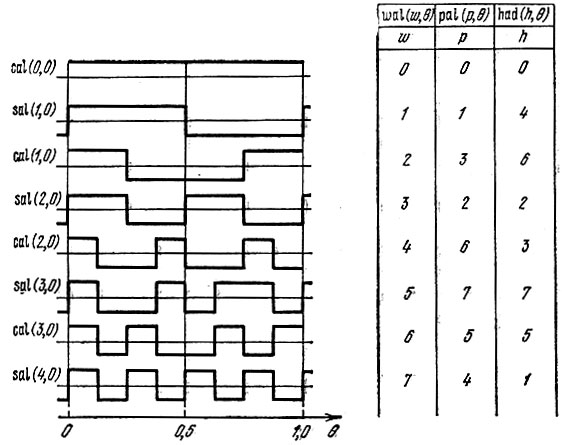
Рис. 14.12. Первые восемь функций Уолша и их нумерация при различных способах упорядочения

Нетрудно также проверить правильность соотношений:

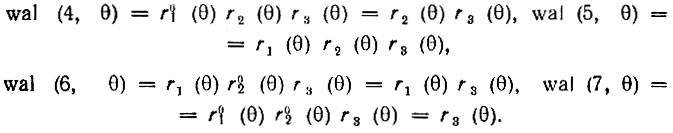
Итак, каждая функция Уолша wal (w, θ), входящая в систему из N = 2ⁿ функций, является произведением степеней первых n функций Радемахера. Принцип нахождения показателей этих степеней поясняется табл. 14.1 на примере N = 2³ = 8.

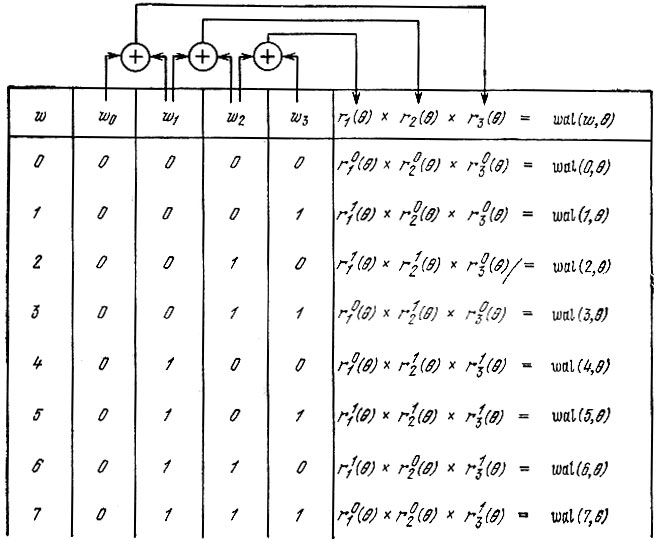
Таблица 14.1

В этой таблице использованы следующие обозначения: w - номер функции в системе; w_m - m-й разряд представления числа w в двоичной системе счисления, т. е.

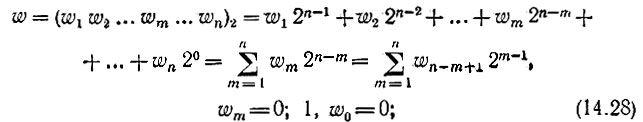
- символ поразрядного суммирования по модулю 2 по правилам

Показанный в табл. 14.1 способ построения функций Уолша можно выразить аналитически для любого N = 2ⁿ в виде следующего соотношения:

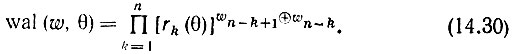
Поясним применение (14.30) на примере шестой функции Уолша (w = 6), входящей в систему размером N = 2³ = 8. Произведение в (14.30) состоит из трех множителей (при k = 1, 2 и 3) вида Подстановкой в левую часть (14.28) w = 6 и n = 3 получаем

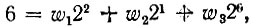
откуда следуют равенства w₁ = 1, w₂ = 1; w₃ = 0. Таким образом,

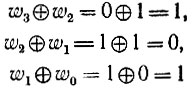
и по формуле (14.30)

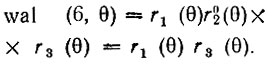
Из рис. 14.12 видно, что четным относительно середины интервала определения (θ = 0,5) функциям wal (w, θ) соответствуют четные номера w, а нечетным функциям - нечетные номера. Такое взаимно однозначное соответствие между четностью функций wal (w, θ) и четностью их номеров w аналогично свойствам тригонометрических функций 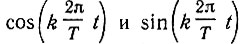(см. рис. 14.13).

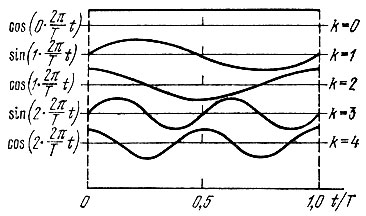
Рис. 14.13. Четность номеров косинусоидальных и нечетность номеров синусоидальных функций

Поэтому иногда применяются обозначения cal (j, θ) для четных и sal (i, θ) для нечетных функций Уолша.

Легко проверить, что функции cal (j, θ) и sal (j, θ) связаны с функциями wal (w, θ) следующими соотношениями:

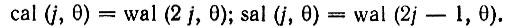
Эти обозначения указаны на рис. 14.12.

Способ нумерации функций в системе называется упорядочением. Функции Уолша, сформированные посредством выражения (14.30), упорядочены по Уолшу.

Часто применяются функции Уолша, упорядоченные по Пэли [pal (р, θ)] и по Адамару [had (h, θ)]^*.

^* (Обозначения pal (р, θ) и had (h, θ) образованы из начальных букв фамилий Paley и Hadamard соответственно.)

Независимо от упорядочения функции Уолша, составляющие систему из N = 2ⁿ функции, всегда можно представить в виде произведения степеней первых n функций Радемахера. Принцип же нахождения показателей этих степеней индивидуален для каждого упорядочения.

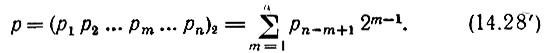
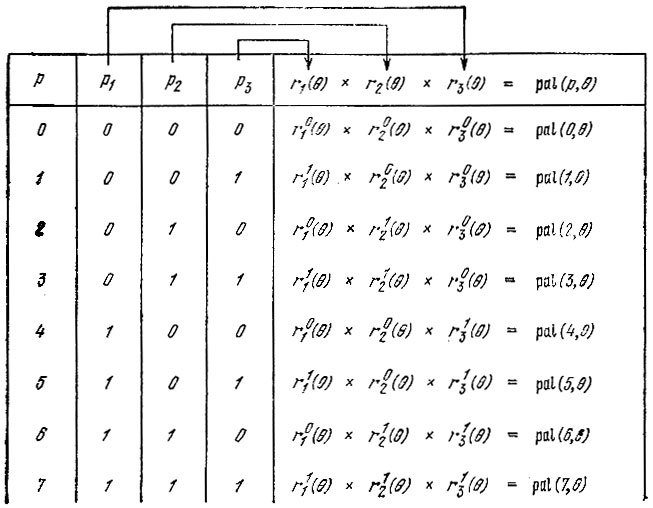
Таблица 14.2

Очевидно, что аналитическая запись функций Уолша в упорядочении Пэли имеет следующий вид:

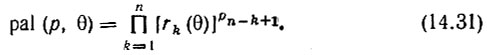
Сравнивая способы образования показателей степеней функций Радемахера на примерах табл. 14.1 и 14.2, легко приходим к выводу, что двоичные разряды номеров функций Уолша, упорядоченных по Пэли, связаны с двоичными разрядами номеров функций Уолша, упорядоченных по Уолшу, следующим соотношением:

Итак, переход от упорядочения по Уолшу к упорядочению этих функций по Пэли выражается в перестановке этих функций в системе по закону (14.32).

Функции had (h, θ) можно сформировать с помощью матриц Адамара. Матрицей Адамара H_N порядка N = 2ⁿ называется квадратная матрица размера N × N с элементами ±1, такая, что

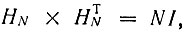
где I - единичная матрица, а т - знак транспонирования.

Нормированную матрицу Адамара порядка N можно построить рекурсивно, т. е.

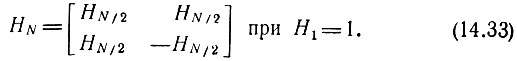
Так, например,

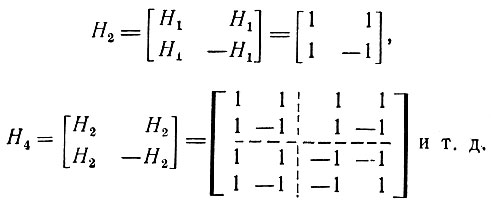
Функция Уолша, упорядоченная по Адамару, т. е. had (h, θ) с номером h, является последовательностью прямоугольных импульсов с единичными амплитудами и полярностями, соответствующими знакам элементов h-й строки матрицы Адамара. Под длительностью импульсов подразумевается (1/N)-я доля интервала [0, 1).

Для иллюстрации связи между функцией had (h, θ) и матрицей Адамара, а также для определения места этих функций в системе приведем матрицу Адамара для N = 8 = 2³, заменяя 1 и -1 знаками соответственно плюс и минус:

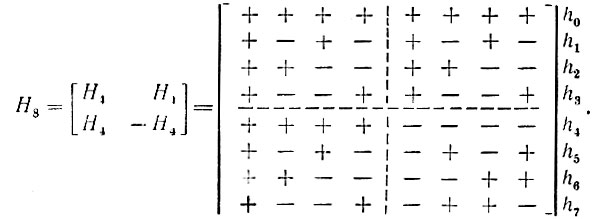
Взаимосвязь между упорядочением по Адамару и Пэли определяется соотношением

где n = log₂ N.

Нумерация первых восьми функций Уолша при различных способах упорядочения дана в табл. на рис. 14.12.

Следует указать, что введенные выше упорядочения вытекают из свойства симметричности матрицы Адамара, заключающегося в том, что транспонированная матрица совпадает с исходной: H_N = H^T_N. Как видно из предыдущего, введенные упорядочения отвечают симметричности соответствующих им матриц.

Не следует полагать, что упорядочениями Уолша, Пэли и Адамара исчерпываются все возможные упорядочения.

Независимо от способа упорядочения функции Уолша в дальнейшем будут обозначаться символом wal (i, θ). Функции Уолша ортонормированы на интервале 0 ≤ θ < 1:

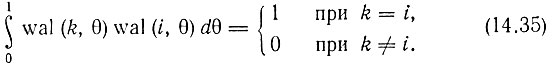
Функции Уолша обладают свойством мультипликативности, т. е. перемножение двух функций Уолша дает другую функцию Уолша, причем

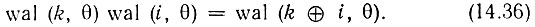
Функции Уолша wal (i, θ) обладает свойством симметрии, проявляющегося в том, что все выводы относительно i справедливы также и относительно θ. Так, например, свойство мультипликативности (14.36) с учетом свойства симметрии запишется в виде

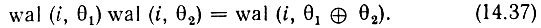
Умножение любой функции Уолша самой на себя дает функцию нулевого порядка wal (0, θ), так как в результате получаются только произведения вида (+1) (+1) и (-1) (-1). Таким образом,

Очевидно также, что умножение wal (i, θ) на wal (0, θ) не изменяет функцию wal (i, θ).

Функции Уолша иногда определяют на интервале -¹/₂ ≤ θ < ¹/₂. Первые восемь функций на указанном интервале представлены на рис. 14.14. Функции Уолша могут служить базисом спектрального (негармонического) представления сигналов.

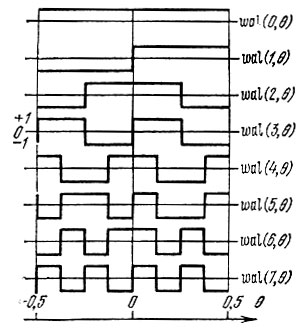
Рис. 14.14. Первые восемь функций Уолша на интервале -0,5 ≤ θ < 0,5

Любую интегрируемую на интервале 0 ≤ θ < 1 функцию f(θ) можно представить рядом Фурье по системе функций Уолша

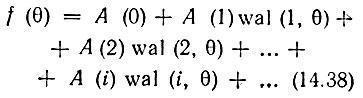
с коэффициентами

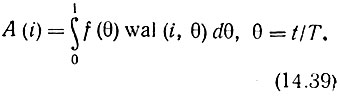
Вне интервала [0, 1) ряд (14.38) описывает периодическую функцию f(θ + k), где k - любое целое число.

На рис. 14.15 изображены первые 16 функций Уолша.

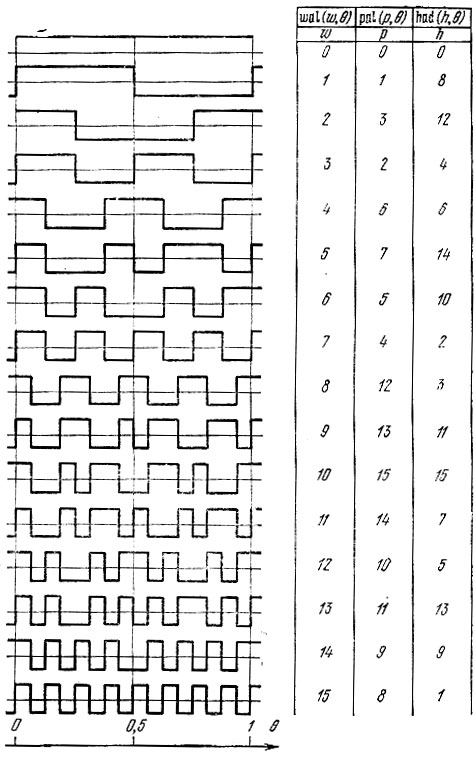
Рис. 14.15. Нумерация функций Уолша при различных способах упорядочения. Размер базиса N = 16

Некоторые особенности разложения непрерывных функций по системе Уолша иллюстрируются в § 14.5 на примерах.

Как уже ранее отмечалось, функции Уолша хорошо сочетаются с современной микроэлектроникой и могут быть легко сформированы с помощью ключевых схем. Один из возможных вариантов схемы генератора первых восьми функций представлен на рис. 14.16.

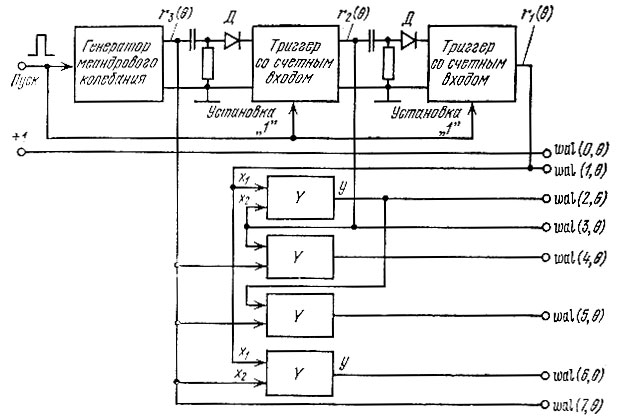
Рис. 14.16. Генератор первых восьми функций Уолша

Алгоритм формирования функций Уолша в этом генераторе основан на выражении (14.30), т. е. на перемножении степеней трех функций Радемахера: r₁(θ), r₂(θ) и r₃(θ). Функция r₃(θ) получается непосредственно от генератора меандрового колебания. Вторая функция r₂(θ) получается из r₃(θ) удлинением периода этого колебания в два раза. Это достигается с помощью триггера, запускаемого положительными импульсами (с выхода дифференцирующей RC-цепи и диода), возникающими в начале каждого периода входного меандра. Аналогичным способом из r₂(θ) получается функция r₁(θ). Полученные функции r₁(θ), r₂(θ) и r₃(θ) поступают либо непосредственно на выход генератора, либо на перемножители Y. Каждый перемножитель представляет собой устройство совпадения, обладающее следующей таблицей истинности:

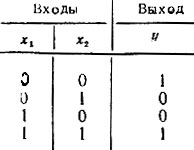
Устройство запускается импульсом, который одновременно устанавливает все триггеры в состояние "1".