
14.6. Взаимный спектр базисных функций двух различных ортогональных систем
Разложим заданное колебание s(t) по двум ортонормированным системам функций φk(t) и ξn(t) с одинаковыми интервалами определения (a, b):
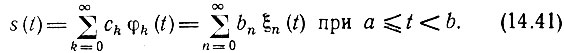
Совокупность коэффициентов ck образует спектр колебания s(t) в базисе φ(t), а совокупность коэффициентов bn - спектр того же колебания s(t) в базисе ξ(t).
Воспользуемся далее выражением (2.9) для коэффициентов сk обобщенного ряда Фурье и подставим в него вместо f(х) заданную функцию s(t), выраженную через правую часть (14.41):
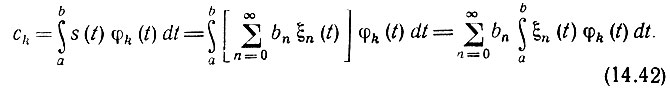
Ввиду ортонормированности функций φk(t) коэффициент перед интегралом в (2.9) приравнен единице. Интеграл под знаком суммы представляет собой k-й коэффициент разложения функции ξn(t) по базисным функциям φk(t). Обозначив этот коэффициент символом
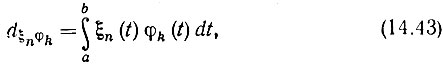
получим

Коэффициенты dξnφk не зависят от сигнала s(t). Таким образом выражение (14.44) устанавливает взаимосвязь спектров колебания s(t) в двух различных базисах φk(t) и ξn(t).
Рассмотрим подробнее выражение (14.43). С одинаковым основанием его можно трактовать либо как k-й коэффициент разложения функции ξn(t) по ортонормированной системе функций φ(t), либо как n-й коэффициент разложения φk(t) по системе функций ξ(t). Поэтому совокупность коэффициентов dξnφk можно рассматривать как взаимный спектр базисных функций φk(t) и ξn(t).
В качестве примера рассмотрим взаимный спектр функций Уолша и тригонометрических функций. Основываясь на выражении вида (14.43), запишем аналогичные выражения отдельно для нечетных и четных функций, определенных на интервале [-1/2, 1/2):
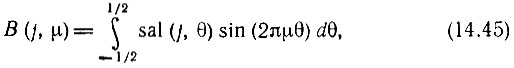
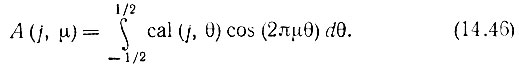
Аргументы тригонометрических функций ωt приведены к виду
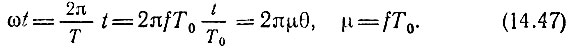
На рис. 14.27 изображен рельеф модуля взаимного спектра (четных) функций Уолша при N = 64 и синусоидальных функций. Видно, что рельеф взаимного спектра В(j, μ) характеризуется хорошо выраженной симметрией. Максимумы |В(j, μ)| находятся вблизи плоскости j = μ. Дополнительные плоскости симметрии, связывающие боковые максимумы, перпендикулярны основной плоскости и пересекают ее с интервалами 2k в точках j = μ = 2k, k = 0, 1, 2, ...
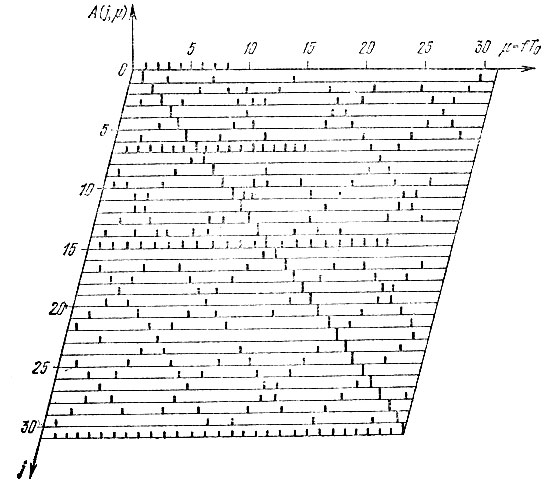
Рис. 14.27. Взаимный спектр функций Уолша и тригонометрических функций (четные компоненты)

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
