14.7. Дискретные функции Уолша

Для цифровых методов спектрального анализа наибольший интерес представляют дискретные функции Уолша. Эти функции являются отсчетами непрерывных функций Уолша. Для перехода к дискретному варианту функций представим аргумент 0 ≤ θ < 1 в двоичной системе счисления

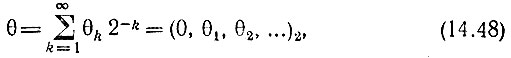
где θ_k = 0, 1, k = 1, 2, 3, ...

При изменении θ в пределах от нуля до единицы k-й разряд θ_k попеременно принимает значения 0 или 1, причем интервал между двумя соседними переменами знаков равен ¹/₂^k. Таким образом, при k = 1 разряд θ₁ равен нулю на интервале 0 ≤ θ < ¹/₂ и равен единице на интервале ¹/₂ ≤ θ < 1. При k = 2 θ₂ = 0 на интервалах 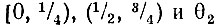= 1 на интервалах 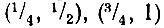и т. д.

Поэтому выражение (14.26) для k-й функции Радемахера можно записать в форме

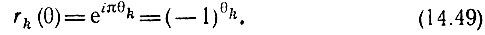
Подставив это выражение в (14.30), получим следующую запись функций Уолша (в упорядочении Уолша):

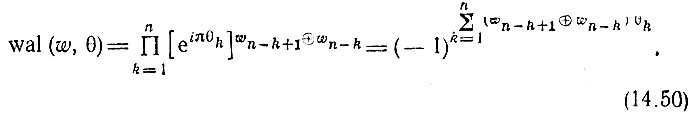
Результат не изменится, если аргумент 0 ≤ θ < 1 заменить целочисленной переменной х = 0, 1, ..., N - 1, являющейся номером отсчета и записанной в двоичной системе счисления

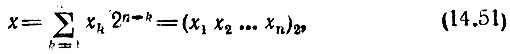
где х_k = 0; 1, k = 1, 2, 3, ..., N = 2ⁿ.

Тогда выражение (14.50) принимает следующий вид:

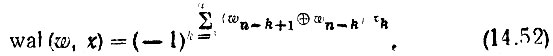
Первые две и последняя (N - 1)-я дискретные функции Уолша, определяемые выражением (14.62), показаны на рис. 14.28 (для N = 16). Каждый отсчет расположен в середине связанного с ним элемента непрерывной функции. Длительность элемента равна 1/N от интервала [0, 1).

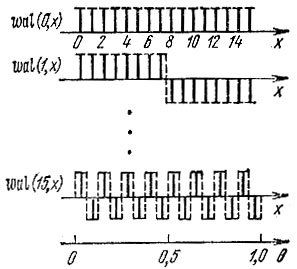
Рис. 14.28. Первые две и последняя дискретные функции Уолша при N = 2³ = 16 (в упорядочении Уолша)

С учетом (14.32) и (14.34) дискретные функции Уолша в упорядочении Пэли и Адамара запишутся в виде

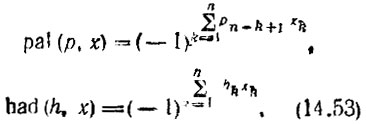
Перечисленные в § 14.4 свойства непрерывных функций Уолша записывается для дискретных функций следующим образом.

Ортогональность

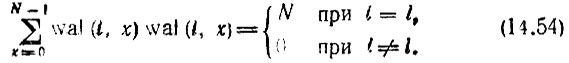
Дискретные функции Уолша не нормированы; норма равна N независимо от номера функции.

Мультипликативность

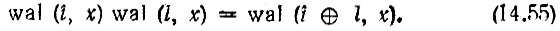
Пусть сигнал s(t) (вещественная функция) представлен совокупностью своих эквидистантных отсчетов s(k), k = 0, 1, 2, ..., N - 1. Тогда преобразования

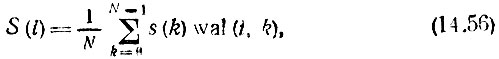
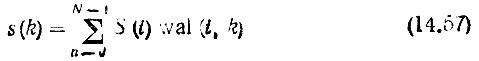
образуют пару дискретных преобразований Уолша (ДПУ). Выражения (14.56), (14.57) аналогичны паре дискретных преобразований Фурье (ДПФ)в базисе гармонических функций [см. (13.13'), (13.14)].

Как и ДПФ (см. § 13.3), ДПУ обладают свойством периодичности:

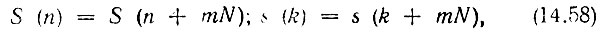
где m - целое число.

Имеются, однако, и существенные особенности ДПУ. Это относится к теореме запаздывания. Напомним, что в случае спектрального анализа в базисе гармонических функций умножение ДПФ S_T(nω₁) на базисную функцию 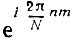эквивалентно сдвигу во времени последовательности s(k), k = 0, 1, 2, ..., N - 1, на m интервалов (см. § 13.3).

В случае ДПУ умножение обеих частей равенства (14.56) на базисную функцию wal (n, m) приводит к выражению

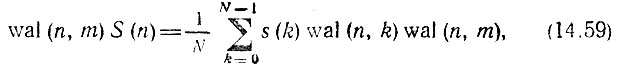
которое на основании свойства мультипликативности функций Уолша [см. (14.36) и (14.37)] можно записать в форме

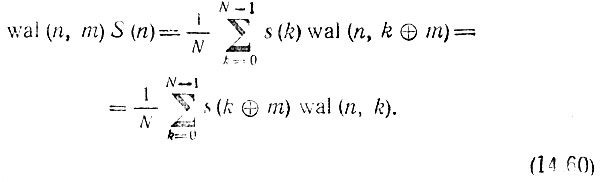
Переход от 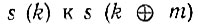означает диадный сдвиг последовательности отсчетов s(k), k = 0, 1, 2, ..., N - 1, на m интервалов.

Аналогично можно показать, что диадному сдвигу спектральных компонентов S(n) на m интервалов соответствует умножение отсчетов s(k) на wal (k, m).

Поясним смысл термина диадный сдвиг. С понятием сдвига функции приходится иметь дело, например, при определении корреляционной функции, при рассмотрении теоремы запаздывания, при определении свертки двух функций. В обычном смысле сдвиг рассматривается как параллельный перенос сдвигаемых значений колебания вдоль оси времени. Такой сдвиг можно назвать арифметическим, так как он выражается обычным арифметическим сложением или вычитанием. При арифметическом сдвиге, например, на m = 3 интервала k-й отсчет x(5) переместится и станет х(5 + 3) = х(8). При достаточно большом m отсчет х(k) выйдет за пределы исходной совокупности отсчетов. При диадном сдвиге тот же отсчет х(5), сдвинутый на m = 3, займет положение 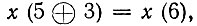так как

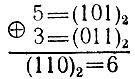
Диадный сдвиг обладает так называемым групповым свойством: сдвиг отсчетов х(k) (где k = 0, 1, 2, ..., N - 1) на величину m ≤ N - 1 соответствует такой перестановке этих отсчетов внутри их исходной совокупности, что результат поразрядного сложения по модулю 2, т. е. 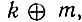всегда не превышает число N - 1 при любом m = 0, 1, 2, ..., N - 1. При этом имеется в виду, что N = 2ⁿ, где n - целое положительное число.

Сделанное утверждение легко проверить перебором всевозможных диадных сдвигов всех отсчетов х(k) при заданном N Например, при N = 8 получается следующая квадратная матрица значений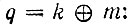

Из этой матрицы видно, что диадный сдвиг не выводит сдвинутые отсчеты за пределы исходной совокупности N отсчетов, а лишь производит их перестановку внутри этой совокупности.

Диадный сдвиг придает существенное своеобразие как спектральному анализу в базисе функций Уолша, так и представлению сигналов во временной области. В частности, диадная свертка двух временных последовательностей х(k) и y(k) записывается в форме

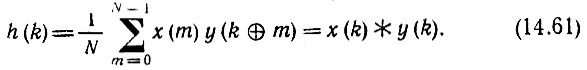
Основное преимущество ДПУ перед ДПФ заключается в том, что отсчеты сигнала умножаются на функции Уолша, которые принимают значения ±1 [см. (14.56), (14.57)]. По существу, операция умножения исключается и выражения (14.56), (14.57) сводятся к суммированию отсчетов с соответствующими знаками. В случае же ДПФ требуется умножение на комплексные числа вида 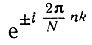причем действительная и мнимая части этих чисел требуют представления достаточно большим числом разрядов (для снижения уровня ошибки округления).

Эффективность цифровых методов спектрального анализа можно значительно повысить, применяя специальные алгоритмы преобразования, получившие название быстрое преобразование Фурье (БПФ), быстрое преобразование Уолша (БПУ) и т. д. Эти алгоритмы основаны на устранении избыточности в описании матрицы дискретного ортогонального преобразования.