15.2. Некоторые свойства передаточной функции четырехполюсника

Из теории линейных электрических цепей известно, что передаточную функцию физического четырехполюсника с сосредоточенными параметрами можно представить в виде рациональной дроби отношения двух полиномов с целыми степенями рис вещественными коэффициентами

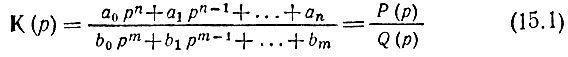
при ряде ограничений на положение корней полиномов Р(р) и Q(р) на p-плоскости, а также на соотношение степеней n и m.

Общим требованием к передаточной функции К(р) любого четырехполюсника, вытекающим из условия устойчивости, является отсутствие полюсов в правой р-полуплоскости (см. § 5.10). Для этого необходимо, чтобы корни полинома Q(p) в знаменателе выражения (15.1) были расположены только в левой р-полуплоскости. Такие полиномы называются полиномами Гурвица.

Далее, для того чтобы рациональная дробь (15.1) являлась передаточной функцией физического четырехполюсника, степень числителя n не должна превосходить степени знаменателя m.

Дополнительные сведения о числе нулей и полюсов функции К(р), а также об их расположении на p-плоскости можно получить из представления выражения (15.1) в форме

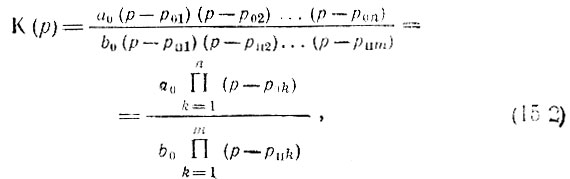
где p_0k - нули функции K(p) [корни уравнения Р(р) = 0], а p_пk - полюса [корни уравнения Q(р) = 0].

Если n = m, то функция К(р) имеет n нулей и nп полюсов при значениях р, равных корням соответственно уравнений Р(р) = 0 и Q(р) = 0. Если n < m, то функция К(р) имеет n нулей в точках p-плоскости, соответствующих n корням уравнения Р(р) = 0 и, кроме того, m - n нулей при р = ∞. Действительно, при р = ∞ выражение (15.2) обращается в

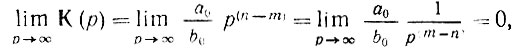
т. е. точка р = ∞ является нулем с кратностью (m - n).

Суммарное число нулей (конечных и бесконечных) равно m. Таким образом, с учетом нулей, расположенных в бесконечности, рациональная функция К(р) имеет равное число нулей и полюсов.

Нули и полюса могут быть вещественными или комплексными. В последнем случае образуются комплексно-сопряженные пары нулей или полюсов. Выражение (15.2) (в отсутствие вещественных нулей и полюсов) можно записать в форме

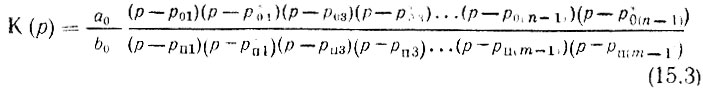
В отличие от полюсов нули передаточной функции могут быть расположены как в левой, так и в правой р-полуплоскости. Четырехполюсники с нулями передаточной функции в правой полуплоскости обладают существенными особенностями, рассматриваемыми в следующем параграфе.