15.3. Связь между амплитудно-частотной и фазочастотной характеристиками четырехполюсника

Анализ прохождения колебания через линейную цепь основан на использовании указанных в заголовке характеристик. Возникает следующий вопрос: можно ли управлять одной из характеристик не изменяя другую или же между ними имеется, однозначное соответствие? Этот вопрос представляет для радиоэлектроники большой практический и научный интерес, особенно при синтезе цепей по заданным амплитудно-частотным и фазочастотным характеристикам.

Вопрос сводится к установлению связи между модулем и аргументом комплексной функции К(р), обладающей следующими свойствами: а) число полюсов конечно; б) полюса в правой полуплоскости р отсутствуют. Этот вопрос приводит к одной из наиболее сложных проблем теории функций комплексного переменного. Значительно более простои задачей является выражение действительной части передаточной функции через мнимую или мнимой через действительную. По лому целесообразно вместо функции К(p) рассматривать функцию θ(р), связанную с К(р) соотношением

На оси частот эта новая функция принимает вид

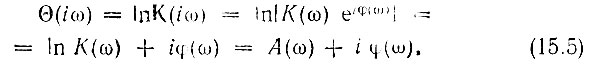
Действительная часть этой функции

называется логарифмическим затуханием четырехполюсника.

Учитывая, что

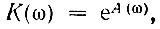
комплексную передаточную функцию можно представить в форме

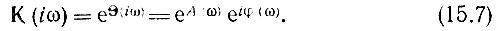
Определяемая выражением (15.5) комплексная функция 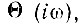характеризующая логарифмическое затухание, а также изменение фазы в четырехполюснике, может быть названа постоянной передачи четырехполюсника по аналогии с термином, применяемым в теории длинных линий.

После перехода от функции К(iω) к функции Θ(iω) задача сводится к установлению связи между А(ω) и φ(ω), т. е. между действительной и мнимой частями комплексной функции Θ(iω).

Воспользуемся для этого следующим равенством, доказываемым в теории функций комплексного переменного:

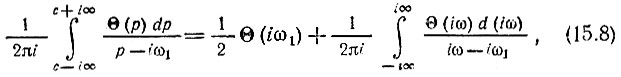
где ω₁ - произвольная фиксированная величина.

Путь интегрирования в левой части этого выражения совпадает с осью iω(с → 0) при обходе точки iω₁ справа. Первое слагаемое в правой части представляет собой половину вычета в точке iω₁, т. е. интеграл по полуокружности бесконечно малого радиуса r. Действительно, на этой окружности функция Θ(р) с точностью до бесконечно малых высшего порядка равна Θ(i, ω₁), знаменатель

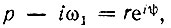
где ψ - аргумент вектора, проведенного из точки iω₁ к точке, лежащей на окружности радиуса r, так что

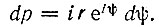
Поэтому интеграл по полуокружности радиуса r равен

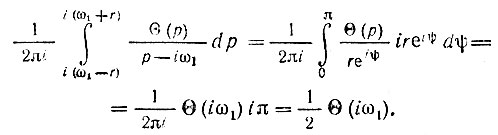
Второе слагаемое в правой части (15.8) - это интеграл по мнимой оси с исключением особой точки iω₁ (главное значение интеграла).

Следует иметь в виду, что с увеличением р (по модулю) и при условии, что Re(р) > 0, функция Θ(р) стремится к нулю. Поэтому интеграл от функции Θ(р)/(р - iω₁) по дуге бесконечно большого радиуса R, лежащей в правой полуплоскости, равен нулю. Это дает основание заменить интеграл, стоящий в левой части равенства (15.8), интегралом по замкнутому контуру, показанному на рис. 15.1.

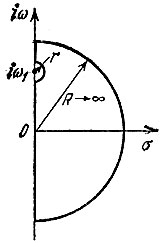
Рис. 15.1. Контур интегрирования на комплексной плоскости

Наложим условие, что функции Θ(р) не имеет полюсов в правой р-полуплоскости. Тогда по теореме Коши интеграл в левой части (15.8) равен нулю. Приравнивая в (15.8) левую часть нулю и, кроме того, заменяя Θ(iω₁) по уравнению (15.5), приходим к выражению

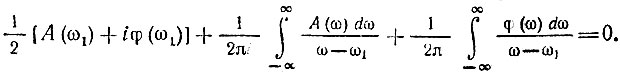
Приравнивая нулю действительные и мнимые части этого выражения, получаем следующие два равенства:

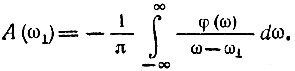
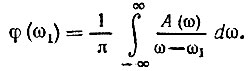
Мы пришли к преобразованиям Гильберта (см. § 3.8). Функция А(ω₁) является сопряженной (по Гильберту) функции φ(ω₁). Так как А(ω) есть четная, а φ(ω) - нечетная функция, то

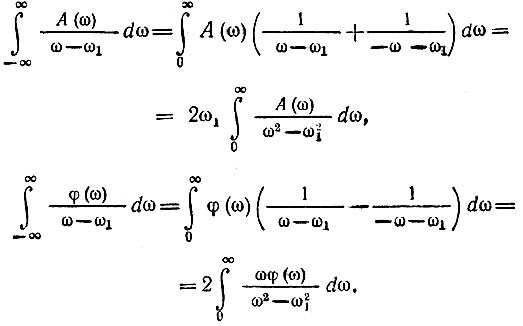
Подставляя эти результаты в предыдущие выражения, приходим к следующим окончательным формулам:

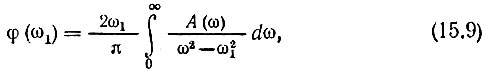
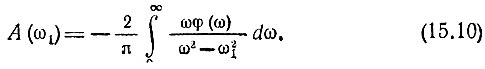
Итак, фазовая характеристика φ(ω₁) при какой-либо фиксированной частоте ω₁ выражается через логарифмическое затухание А(ω), причем последнее интегрируется в пределах от ω = 0 до ω = ∞. Аналогичное правило относится и к логарифмическому затуханию. Таким образом, для определения одной из характеристик на какой-либо частоте необходимо знать изменение другой во всем частотном диапазоне.

Переходя в выражении (15.9) от А(ω) к К(ω) по формуле (15.6), получаем искомую зависимость между фазовой и амплитудно-частотной характеристиками:

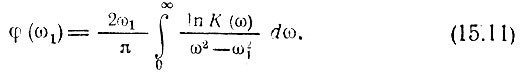
Оговоренное ранее условие отсутствия полюсов функции Θ(р) в правой полуплоскости равносильно условию отсутствия полюсов и нулей функции К(р) в этой же полуплоскости (так как в точках плоскости р, где К(р) равно нулю, ln К(ω) обращается в - ∞).

Поэтому можно сформулировать следующее важное положение: однозначное соответствие между амплитудно-частотной и фазовой характеристиками имеется только у четырехполюсников, передаточная функция которых К(р) не имеет нулей в правой полуплоскости р.

Четырехполюсники, соответствующие этому условию, называются минимально-фазовым и. К таковым относятся обычные колебательные цепи, фильтры и цепи, в которых отсутствуют перекрестные связи. К неминимально-фазовым относятся мостовые и некоторые другие специального вида цепи.

Итак, если требуется, чтобы синтезируемый четырехполюсник являлся минимально-фазовым, передаточная функция К(р) не должна иметь нулей в правой p-полуплоскости. В этом случае оба полинома Р(р) и Q(р) в выражении (15.1) должны являться полиномами Гурвица.

Остановимся на некоторых свойствах характеристик минимально-фазовых четырехполюсников. Из выражений (15.9), (15.10) видно, что величины входящих в них интегралов определяются характером изменения А(ω) и φ(ω) вблизи частоты ω₁, так как при удалении ω от ω₁ абсолютная величина дроби 1/(ω² - ω²₁) быстро убывает. Заметим, что интеграл от этой дроби, меняющей свой знак в точке ω = ω₁, взятый в пределах от 0 до ∞, равен нулю^*. Поэтому, если допустить, что для некоторой физической цепи затухание А(ω) = А₀, т. е. является постоянной величиной для всех частот от 0 до ∞, то

^* (Имеется в виду главное значение интеграла с исключением особой точки.)

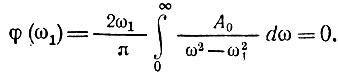
Следовательно, равномерное для всего диапазона логарифмическое затухание (а следовательно, и равномерную амплитудно-частотную характеристику) можно получить только для цепи, фазовая характеристика которой равна нулю, т. е. если цепь состоит из чисто омических сопротивлений.

С другой стороны, добавление к затуханию A(ω) постоянной величины A₀ не изменяет фазовой характеристики, так что выражение (15.9) можно записать в более общей форме

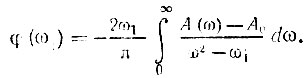
Физически это означает лишь изменение масштаба амплитудно-частотной характеристики с помощью, например, усилителя, имеющего равномерную амплитудно-частотную характеристику, или с помощью делителя напряжений (потенциометра), составленного из чисто омических сопротивлений. (В первом случае A₀ нужно брать со знаком плюс, во втором - со знаком минус.)

Можно также показать, что если вблизи рассматриваемой частоты ω₁ функция A(ω) изменяется слабо, то определяемая выражением (15.9) фазовая характеристика изменяется линейно; участкам же диапазона с относительно быстрым изменением A(ω) соответствует нелинейное изменение φ(ω). Иными словами, участкам, с равномерной амплитудно-частотной характеристикой соответствует линейная фазочастотная характеристика.

Кроме того, при прохождении К(ω) через максимум, т. е. в полосе прозрачности цепи, наклон фазовой характеристики отрицателен 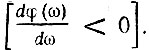Соответственно при прохождении через минимум (в полосе непрозрачности) наклон фазовой характеристики положителен 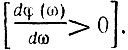Эти положения хорошо иллюстрируются, в частности, амплитудно-частотными и фазовыми характеристиками колебательных цепей, рассматривавшихся в § 5.7 (например, резонансная и фазовая характеристики на рис. 5.18).