15.4. Представление четырехполюсника общего вида каскадным соединением элементарных четырехполюсников

При заданных нулях и полюсах передаточную функцию К(р) целесообразно представлять в виде произведения множителей, каждый из которых может являться передаточной функцией простейшего, элементарного четырехполюсника. Пусть, например, передаточная функция синтезируемого четырехполюсника

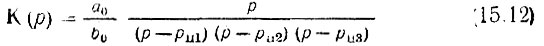
обладает нулем в точке р = 0 и тремя полюсами, из которых один вещественный в точке р_п1 < 0 и два комплексных: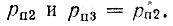

Учитывая равенство

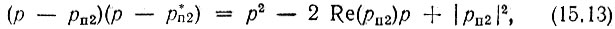
записываем (15.12) в форме

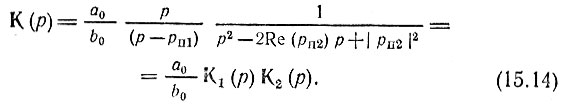
Передаточная функция К₁(р) реализуется звеном первого порядка (RC-цепь или RL-цепь). Действительно, для RС-цепи (рис. 6.6, а) при съеме напряжения с резистора передаточная функция

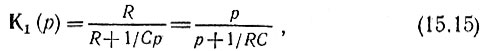
откуда следует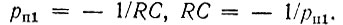

При использовании RL-цепи (рис. 6.7, а)

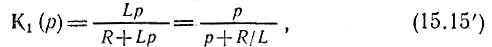
откуда p_п1 = -R/L.

Функция К₂(р) реализуется звеном второго порядка. Этот вопрос подробно рассматривается в следующем параграфе.

При синтезе неминимально-фазового четырехполюсника разбиение его передаточной функции на простые множители имеет некоторые особенности. Поясним их на примере функции

где р₀₁ - вещественная положительная величина, а р_п1 - вещественная, но отрицательная величина (рис. 15.2).

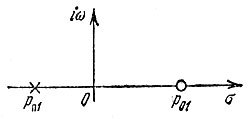
Рис. 15.2. Расположение нуля и полюса на р плоскости для неминимально-фазового четырехполюсника

Умножим числитель и знаменатель в (15.16) на р + р₀₁. Тогда

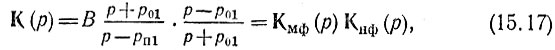
где

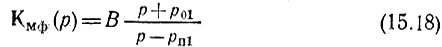
обозначает передаточную функцию минимально-фазового четырехполюсника (поскольку нуль расположен в точке р = -р₀₁, т. е. в левой полуплоскости), а

- передаточную функцию четырехполюсника неминимально-фазового типа.

Правая часть выражения (15.17) соответствует передаточной функции двух каскадно-соединенных четырехполюсников. Следовательно, рассматриваемый четырехполюсник с передаточной функцией К(р), определяемой выражением (15.16), можно заменить эквивалентным каскадным соединением двух четырехполюсников К_мф(р) и К_нф(р) (рис. 15.3).

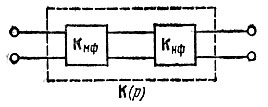
Рис. 15.3. Схема замещения четырехполюсника с нулем в правой р-полуплоскости

Рассмотрим подробнее второй четырехполюсник К_нф. Переходя от р к iω, записываем эту функцию в виде

Так как р₀₁ - действительное число, то модуль этой функции равен единице на всех частотах от ω = 0 до ∞. Аргумент же

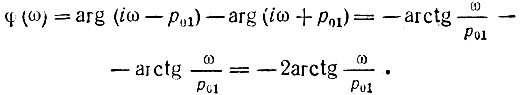
Таким образом, передаточная функция

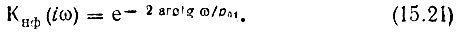
Итак, четырехполюсник с передаточной функцией вида (15.20) должен пропускать (равномерно) все частоты от 0 до ∞. Такие четырехполюсники, позволяющие осуществлять коррекцию фазочастотной характеристики при неизменной амплитудно-частотной, называются фазокорректирующими контурами. Реализация таких цепей рассматривается в § 15.6.

Трактовка выражения (15.14) как передаточной функции каскадного соединения взаимно независимых четырехполюсников К₁(р) и К₂(р) позволяет задачу синтеза сложного четырехполюсника свести к синтезу простых звеньев. Увеличение числа нулей и полюсов в передаточной функции приводит лишь к соответствующему увеличению числа звеньев. Естественно, такой подход имеет смысл и допустим лишь при достаточной развязке элементарных четырехполюсников. Применение эмиттерных повторителей и некоторых других устройств современной микроэлектронной техники обеспечивает выполнение этого требования. В тех случаях, когда нельзя пренебрегать взаимным влиянием элементарных четырехполюсников, приходится прибегать к более сложным методам синтеза, излагаемым в специальной литературе [7-9].