15.5. Реализация типового звена второго порядка

Передаточную функцию элементарного четырехполюсника в соответствии с (15.14) зададим в форме

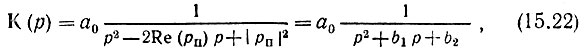
где постоянные коэффициенты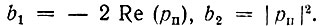

Рассмотрим сначала реализацию функции К(р) с помощью цепи, содержащей катушку индуктивности L, конденсатор С и резистор R (рис. 15.4). Сопротивление резистора, являющегося нагрузкой четырехполюсника, считаем заданным. Один из элементов цепи Z₁₂, Z₂ должен быть индуктивным, а другой - емкостным. Под источником тока, возбуждающим цепь, можно подразумевать, например, коллекторную цепь транзисторного усилителя, работающего по схеме ОЭ (см. § 5.4, рис. 5.12, б). Внутренней проводимостью источника тока пренебрегаем. Величина тока I, равна SЕ₁, где Е₁ - напряжение база - эмиттер.

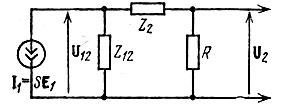
Рис. 15.4. Реализация типового звена второго порядка

Напряжение на элементе Z₁₂ можно определить выражением

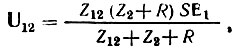
а напряжение на резисторе R выражением

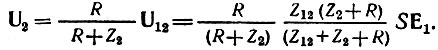
Следовательно,

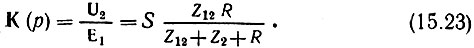
Из сопоставления этого выражения с (15.22) очевидно, что для получения вещественного числителя следует задать Z₁₂ = 1/Ср и Z₂ = Lp. При этом получим

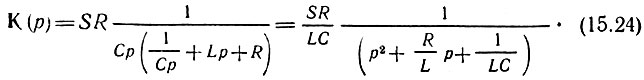
Сравнение (15.24) с (15.22) приводит к равенствам

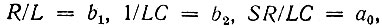
откуда

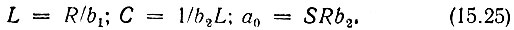
Таким образом, схема искомой цепи принимает вид, показанный на рис. 15.5, а.

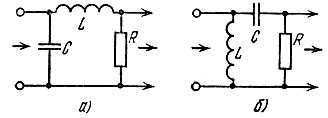
Рис. 15.5. Реализация передаточной функции: а - по выражению (15.24); б - по выражению (15.26)

Аналогичным образом нетрудно показать, что передаточной функции вида

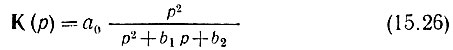
соответствует схема, представленная на рис. 15.5, б, параметры которой L и С выражаются через коэффициенты b₁ и b₂ теми же соотношениями (15.25), что и в схеме на рис. 15.5, а. Различие лишь в постоянном коэффициенте а₀ = SR₁.

В интегральных схемах, не допускающих применения катушек индуктивности, цепь второго порядка реализуется с помощью активной RС-цепи. Один из возможных вариантов такой цепи представлен на рис. 15.6, а. Свойства этой цепи обусловлены применением операционного усилителя К₀ и обратной связи. Усилитель в рассматриваемой схеме должен обеспечить весьма небольшое усиление (не более нескольких единиц). Основные требования к усилителю - очень большое входное и близкое к нулю выходное сопротивление а также отсутствие обратной реакции. При выполнении этих требований усилитель можно рассматривать как идеальный источник напряжения (управляемый напряжением), что позволяет при определении токов и напряжений в схеме на рис. 15.6, а считать точки а и б разомкнутыми, а напряжение на выходе приравнивать величине K₀U_С2, где U_С2 - напряжение на конденсаторе С₂. Эти допущения приводят к эквивалентной схеме на рис. 15.6, б, на которой усилитель К₀ опущен, а его влияние учтено тем, что напряжение на конденсаторе С₂ связано с выходным напряжением соотношением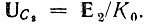

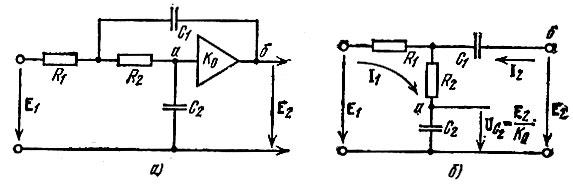
Рис. 15.6. Активная RС-цепь второго порядка (а) и схема замещения (б)

Применяя общие уравнения четырехполюсника (5.4) к схеме, представленной на рис. 15.6, б, и учитывая добавочное условие

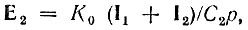
получаем

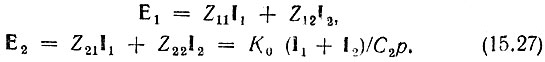
Здесь

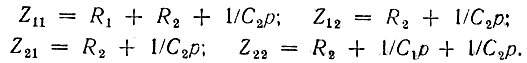
Исключив ток I₂ из первого уравнения (15.27), после несложных преобразований получим следующее выражение для передаточной функции четырехполюсника:

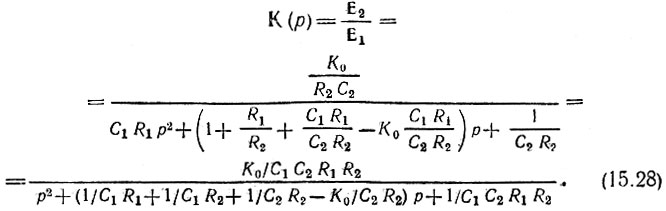
Дальнейшая задача синтеза сводится к подбору резисторов, конденсаторов и усиления К₀, обеспечивающих требуемые значения коэффициентов b₁ и b₂ полинома (15.22):

Из первого равенства можно получить следующее выражение для требуемого коэффициента усиления:

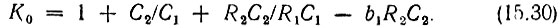
Полученные соотношения будут проиллюстрированы в § 15.8.