15.6. Реализация фазокорректирующей цепи

Неминимально-фазовые четырехполюсники с равномерной в диапазоне 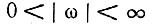амплитудно-частотной характеристикой реализуются с помощью мостовых схем. Простая цепь подобного типа, составленная из конденсаторов и резисторов, была описана в § 14.2. Недостатком ее является требование бесконечно большого сопротивления нагрузки, подключаемой к диагонали моста 2-2' (см. рис. 14.5). От этого недостатка свободна мостовая схема, составленная из катушек индуктивности и конденсаторов при соответствующем подборе сопротивления нагрузки R_н. В схемах на рис. 15.7 а и б, различающихся лишь начертанием, проводимость Y_н равна 1/R_н, а проводимости ветвей моста Y_a и Y_b выбираются из условия

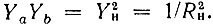
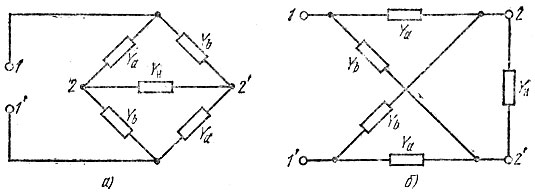
Рис. 15.7. Симметричный мостовой четырехполюсник в разном начертании

Для определения передаточной функции рассматриваемого четырехполюсника воспользуемся схемой замещения, представленной на рис. 5.4, а. Тогда по уравнению (5.13)

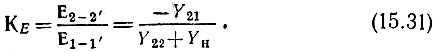
Проводимость Y₂₂ находим в режиме короткого замыкания зажимов 1-1' (рис. 15.8, а). Очевидно, что

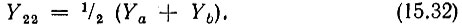
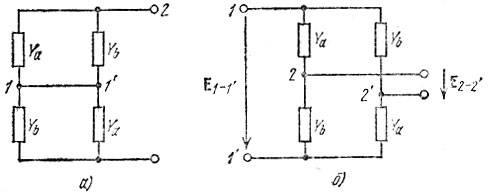
Рис. 15.8. Схемы замещения мостового четырехполюсника: а - при коротком замыкании входа; б - при разомкнутом выходе

Так как схема симметрична, можно также написать

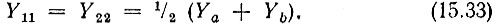
Проводимость 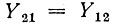легко определяется из выражения для передаточной функции в режиме холостого хода (Y_н = 0, рис. 15.8, б):

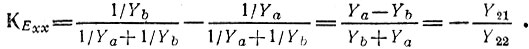
Подставив Y₂₂ по выражению (15.32), получим

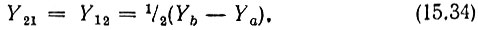
На основании (15.32) и (15.34) выражение (15.31) приводится к виду

а с учетом равенства Y_b = Y²_нY_a

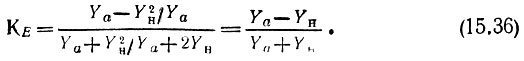
Переходя от проводимостей к сопротивлениям, получаем

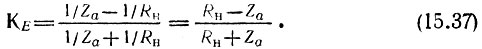
Если сопротивление Z_a образовано емкостью, а Z_b - индуктивностью (рис. 15.9, а), то Z_a = 1/Ср и Z_b = Lp. При этом

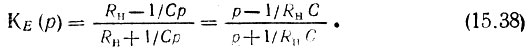
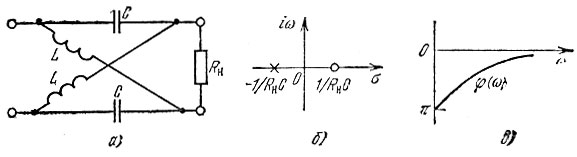
Рис. 15.9. Мостовой четырехполюсник: а - схема; б - положение нуля и полюса на р-плоскости; в - фазочастотная характеристика

Таким образом, нуль передаточной функции р₀ = 1/R_нC, а полюс р_п = -1/R_нC (рис. 15.9, б).

Переходя от р к iω, получаем

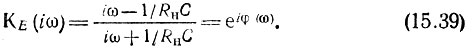
Амплитудно-частотная характеристика К_F(ω) = 1, а фазочастотная (рис. 15.9, в)

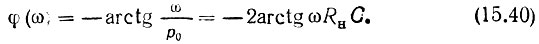
Итак, если заданы нуль передаточной функции р₀ > 0 и сопротивление нагрузки R_н, то элементы мостового звена (рис. 15.9, а) определяются соотношениями

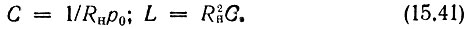
Важным параметром четырехполюсника, особенно при использовании его в каскадной схеме, является входное сопротивление (проводимость). Составив выражение для входной проводимости, аналогичное (5.23), и подставив в него Y₁₁ и Y₂₁ = Y₁₂ по формулам (15.33) и (15.34), нетрудно убедиться, что

Таким образом, входная проводимость согласованно-нагруженного мостового четырехполюсника 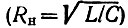независимо от частоты равна 1/R_н.

Для реализации неминимально-фазового четырехполюсника с двумя комплексно-сопряженными нулями в правой р-полуплоскости можно использовать мостовую схему, показанную на рис. 15.10, а.

В этой схеме

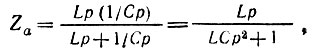
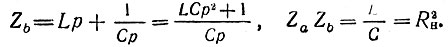
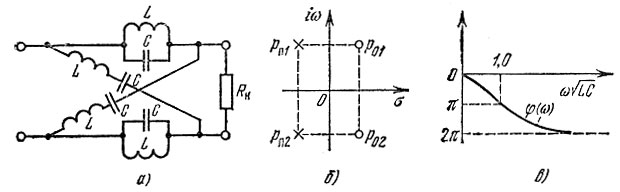
Рис. 15.10. Мостовой четырехполюсник: а - схема; б - положение нулей и полюсов на р-плоскости; в - фазочастотная характеристика

Передаточная функция

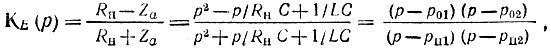
где нули передаточной функции

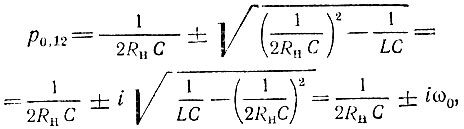
а полюса

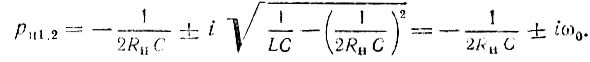
Полюса и нули передаточной функции расположены симметрично относительно оси iω (рис. 15.10, б).

На оси частот передаточная функция

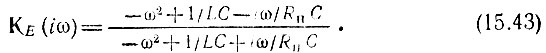
Как и в предыдущей схеме, К_E(ω) = 1. Фазочастотная характеристика (рис. 15.10, в) легко приводится к виду

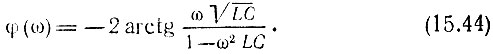
Мостовые четырехполюсники находят широкое применение при синтезе цепей с амплитудно-частотными и фазочастотными характеристиками, неосуществимыми с помощью минимально-фазовых четырехполюсников.

При синтезе цепей, согласованных с заданным сигналом, также приходится применять неминимально-фазовые цепи, поскольку между модулем и аргументом спектральной плотности сигнала необязательно существует однозначная связь. Например, в рассмотренных в гл. 12 согласованных фильтрах применялись линии задержки, передаточные функции которых имеют вид 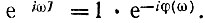Однако классическая теория синтеза электрических цепей, как отмечалось в § 15.1, не применима к подобным цепям.