15.7. Особенности синтеза четырехполюсника по заданной амплитудно-частотной характеристике

При синтезе фильтров нижних частот, фильтров верхних частот, полосовых фильтров и т. д. к фазовым характеристикам обычно не предъявляется каких-либо специфических требований. Предполагается, что обеспечение удовлетворительной равномерности АЧХ минимально-фазового четырехполюсника в заданной полосе частот одновременно обеспечивает также и линейность фазочастотной характеристики в этой полосе.

Основываясь на общем выражении (15.1), представим комплексную передаточную функцию К(iω) в форме

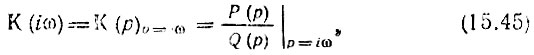
после чего перейдем к квадрату модуля

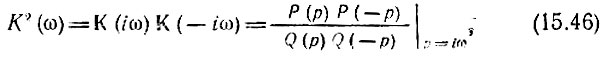
тем самым исключая из рассмотрения фазочастотную характеристику четырехполюсника.

Модуль передаточной функции, четный относительно частоты, можно рассматривать как функцию ω². То же относится к модулям |Р(iω)| и |Q(iω)|. Поэтому выражение (15.46) можно записать в форме

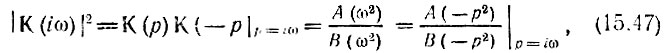
где обозначено

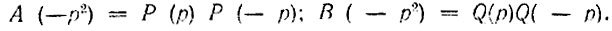
Переходя от мнимой iω к любой точке p-плоскости, получаем следующее выражение:

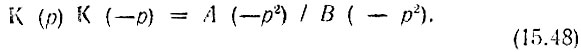
Полюса и нули функции 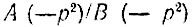расположены в квадрантной симметрии: каждой комплексно-сопряженной паре в левой р-полуплоскости соответствует зеркальная пара в правой полуплоскости,

Поясним это положение на примере простейшего четырехполюсника (рис. 15.11) с передаточной функцией

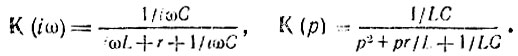
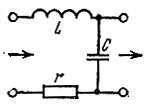
Рис. 15.11. Простой четырехполюсник с двумя полюсами

Комплексно-сопряженной функции К(-iω) соответствуют выражения

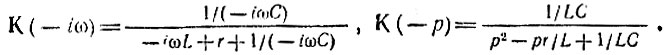
Следовательно,

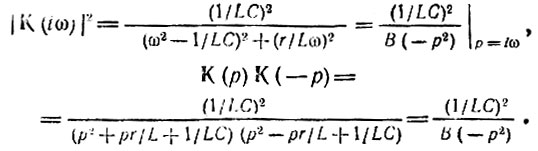
Полюса функции 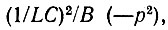являющиеся корнями уравнения В(-р²) = 0, расположены в точках (рис. 15.12)^*

^* (Здесь и в последующих параграфах опущен индекс "п" в обозначении полюса р_пk.)

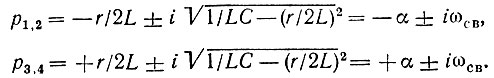
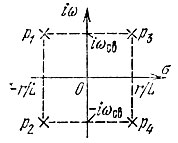
Рис. 15.12. Квадратная симметрия полюсов

К передаточной функции К(р) относятся полюса, расположенные только в левой р-полуплоскости (в данном примере р₁ и р₂). То же относится к нулям передаточной функции, т. е. к корням уравнения А(-р²) = 0 (в данном примере нули отсутствуют), если передаточная функция К(р) соответствует минимально-фазовой цепи. В противном случае нули могут быть расположены и в правой р-полуплоскости.

Следует также указать, что полюса, расположенные на мнимой оси, могут быть только кратными (с кратностью 2). Половина из них должна быть отнесена к К(р), а другая половина к К(-р).

Из перечисленных свойств функции К²(ω) вытекает, что для аппроксимации заданной АЧХ четырехполюсника можно использовать функции, зависящие от ω², а при переходе к переменному р = σ + iω - функции, соответствующие указанному выше расположению полюсов и нулей на р-плоскости.