15.8. Синтез фильтра нижних частот. Фильтр Баттерворта

Амплитудно-частотная характеристика идеального фильтра нижних частот представлена на рис. 15.13. При аппроксимации АЧХ на оси абсцисс обычно откладывается безразмерная (нормированная) частота х = ω/ω_с, где ω_с - частота среза, а по оси ординат - нормированное значение К(ω/ω_с) = К(х).

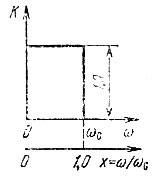
Рис. 15.13. Амплитудно-частотная характеристика идеального фильтра нижних частот

Аппроксимирующую функцию для идеальной характеристики фильтра нижних частот, показанной на рис. 15.13, задают в виде

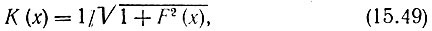
причем накладывают условие, чтобы функция F(x) по модулю была минимальна в полосе 0 < х ≤ 1 и максимальна при х > 1.

Простейшей функцией, отвечающей этому требованию, является функция F(х) = хⁿ - (ω/ω_с)ⁿ. При этом

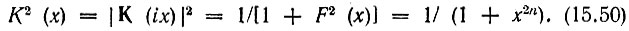
Графики функции (15.49) при нескольких значениях n показаны на рис. 15.14. Определяемая выражением (15.50) аппроксимирующая функция получила название функции Баттерворта, а фильтры, синтезированные на основе этой функции, называются фильтрами Баттерворта. При частоте среза х = 1 (ω = ω_с) функции Баттерворта любого порядка n равны 1/2, что соответствует ослаблению АЧХ до 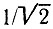(на 3 дБ). Аппроксимацию по Баттерворту часто называют максимально плоской.

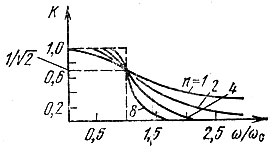
Рис. 15.14. Аппроксимирующие функции Баттерворта

При исчислении К(х) в децибелах выражение (15.49) приводится к виду

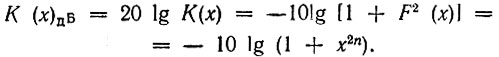
Если безразмерную частоту х представить в виде степени числа 2, т. е. х = 2^у, где у - число октав, то получим

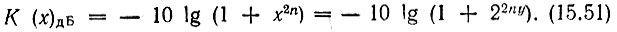
График зависимости К в децибелах от величины у показан на рис. 15.15. На частоте среза (х = 1, у = 0) затухание равно 3 дБ независимо от порядка n.

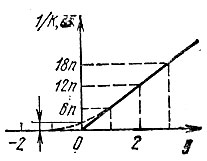
Рис. 15.15. Затухание в фильтре Баттерворта в зависимости от числа октав

Вне полосы прозрачности фильтра, при x²ⁿ >> 1 (у > 1), выражение (15.51) определяет прямую линию

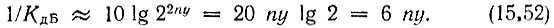
Таким образом, ослабление АЧХ равно 6n_дБ на одну октаву (т. е. при изменении частоты х вдвое, а у - на одну единицу).

Для удовлетворительной аппроксимации прямоугольной характеристики (рис. 15.13) с помощью функции Баттерворта требуются относительно высокие значения n. Так, например, если необходимо, чтобы при ω = 3 ω_с (х = 3) ослабление (затухание) АЧХ было не менее 40 дБ, то n ≥ 40/6y. В данном случае p = lg x/lg 2 = 1,58 и, следовательно, n ≥ 4,25, т. е. требуется n = 5.

Следующим шагом после определения порядка фильтра n является нахождение полюсов передаточной функции, Для этого выразим (15.50) в форме (15.47), для чего в (15.50) приравняем ix = р, х² = -р² и х²ⁿ = (-1)ⁿ р²ⁿ:

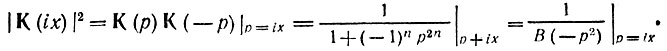
Рассматривая теперь поведение функции 1/В (-р²) на p-плоскости, находим полюса как корни уравнения

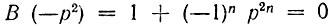
или

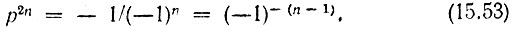
С помощью соотношений

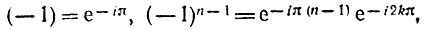
где k - любое целое число, получаем для k-го корня уравнения (15.53) следующее выражение:

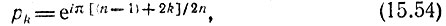
причем число корней равно степени уравнения (15.53).

Модули всех полюсов р_k равны единице, а аргументы

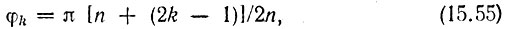
а разность аргументов любых двух соседних корней равна π/n. Следовательно, все полюса функции 1/В (-р²) лежат на окружности единичного радиуса и делят эту окружность на равные дуги π/n. Аргумент первого полюса φ₁ = π (n + 1)/2 n, а последнего φ_2n = π (5n - 1)/2 n.

Расположение полюсов на окружности единичного радиуса для фильтра Баттерворта третьего (n = 3) и четвертого (n = 4) порядков показано на рис. 15.16.

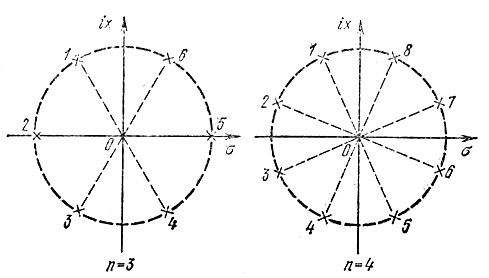
Рис. 15.16. Расположение полюсов передаточной функции фильтра Баттерворта третьего и четвертого порядков

В соответствии с § 15.7 к передаточной функции синтезируемого фильтра относятся только полюса, расположенные в левой полуплоскости.

Эти полюса

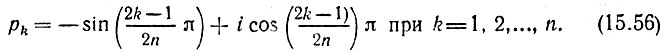
Следует помнить, что формулы (15.53)-(15.55) определяют значения нормированных переменных р, т. е.

Все полюса образуют комплексно сопряженные пары, кроме одного полюса на вещественной оси при нечетном n. Этому единственному полюсу соответствует k = (n + 1)/2. Подставив p_k по формуле (15.54) в общее выражение (15.2), получим передаточную функцию фильтра Баттерворта. Приведем эти выражения для n = 2, 3 и 4.

При n = 2 полюса: 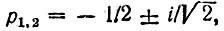и по формулам (15.13) и (15.22) находим

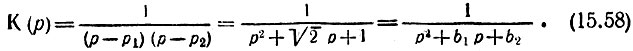
При n = 3 полюса р₁ = -0,5 + i 0,5; р₂ = -1; р₃ = -0,5 - i 0,5 = р₁*.

Передаточная функция

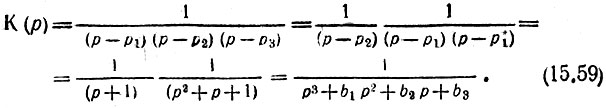
При n = 4 передаточная функция приводится к виду

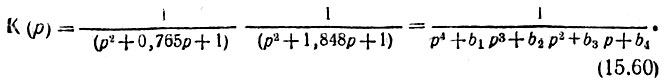
Коэффициенты полиномов в знаменателе передаточной функции Баттерворта приводятся во многих пособиях по расчету фильтров [8, 12].

Последним этапом синтеза фильтра нижних частот является подбор элементов для типовых звеньев второго порядка, а при нечетных n - дополнительно для одного звена первого порядка.

Приведем пример синтеза фильтра Баттерворта второго порядка (n = 2), представляющего собой одно звено с передаточной функцией

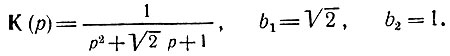
Переходя в выражении (15.28) к нормированной частотной переменной р = (σ + iω)/ω_с (как и в (15.58)), приводим его к виду

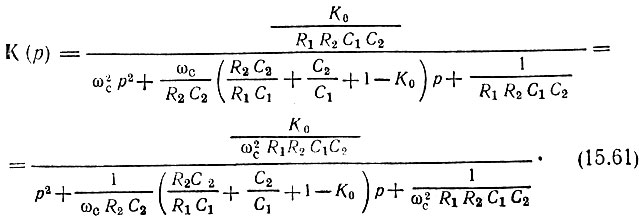
Приравнивая знаменатели в выражениях (15.58) и (15.61), получаем следующие условия для определения параметров схемы:

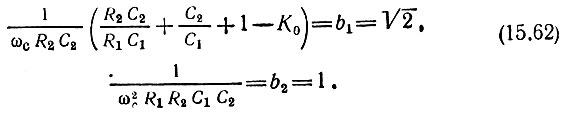
Постоянную времени цепи R₂C₂ обычно приравнивают величине, близкой к 1/ω_с 110, 111. Тогда и ω_cR₁C₁ ≈ 1 (из второго условия (15.62)); при этом первое условие (15.62) сводится к равенству

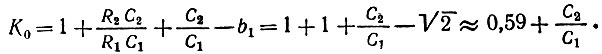
Задавая C₂/C₁ = 0,4, и, следовательно, R₂R₁ = 2,5, получаем K₀ ≈ 1. В данном примере операционный усилитель по существу сводится к эмиттерному повторителю.

Для количественной оценки параметров фильтра нижних частот зададим частоту среза f_c = 1000 Гц, а емкость конденсатора С₂ = 0,1 мкФ. Тогда

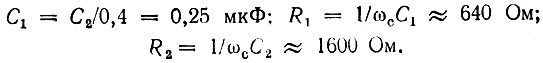
Приведенный выше пример реализации фильтра второго порядка является лишь иллюстрацией. Для выбора оптимальной схемы и проведения инженерного расчета читатель должен обратиться к специальной литературе, например к работам [10, 11].