15.9. Фильтр Чебышева (нижних частот)

Для улучшения аппроксимации идеальной прямоугольной характеристики фильтра нижних частот (рис. 15.13) часто применяется аппроксимация по Чебышеву, при которой в качестве функции F(х) в формуле (15.49) используется квадрат полинома Чебышева Т_n(х) соответствующего порядка n. При этом формула (15.50) записывается в виде

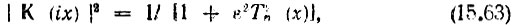
где х = ω/ω_c.

Коэффициент ε < 1 вводится для ограничения амплитуды пульсации АЧХ в полосе пропускания, т. е. в интервале |х| ≤ 1. Чем меньше ε, тем лучше аппроксимируется АЧХ в указанной полосе, но одновременно снижается крутизна ската характеристики в полосе задерживания (при х > 1). Варьируя величину коэффициента ε и степень полинома n, можно осуществить приемлемый компромисс между противоречивыми требованиями к аппроксимации характеристики в полосе пропускания и вне этой полосы.

В § 14.2 указывалось, что значение Т_n(х) колеблется в пределах ±1 в интервале |х| < 1 и растет по закону Т_n(х) ≈ 2^n-1 хⁿ при |х| >> 1. График функции |K(ix)| при ε² = ¹/₅ и n = 4 построен на рис. 15.17.

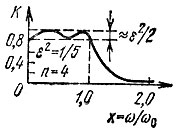
Рис. 15.17. Амплитудно-частотная характеристика фильтра Чебышева четвертого порядка

Амплитуду пульсации АЧХ в полосе пропускания, равную

при малых значениях ε можно приравнять величине ∼ ε²/2 (рис. 15.17).

Вне полосы пропускания, при больших значениях х, когда 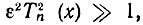передаточная функция монотонно убывает по закону

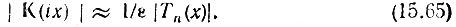
Дня сравнения чебышевской аппроксимации прямоугольной АЧХ с аппроксимацией по Баттерворту найдем ослабление АЧХ при х = 3 для фильтра четвертого порядка n = 4, ε² = 1/5. По формуле, приведенной в § 14.2 (или из таблицы полиномов Чебышева), определяем

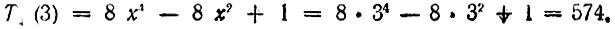
Далее,

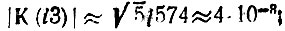
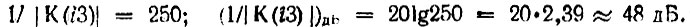
Как видим, при одной и той же степени сложности фильтра (при одинаковых значениях n = 4) ослабление АЧХ у Чебышевского фильтра на 8 дБ больше, чем у фильтра Баттерворта. При этом аппроксимация АЧХ в полосе пропускания лучше у Чебышевского фильтра: наибольшее отклонение от единицы не превышает ε²/2 = -0,1 (вместо ~0,3 у фильтра Баттерворта).

Определим полюса передаточной функции фильтра Чебышева (нижних частот). Как и в предыдущем параграфе, записываем выражение (15.63) в форме

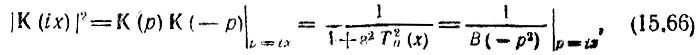
после чего находим корни уравнения

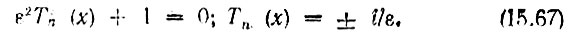
Опустив промежуточные выкладки (см. [6, 7]), приведем окончательные выражения

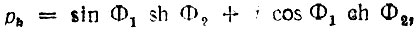
где Ф₁ и Ф₂ определяются формулами

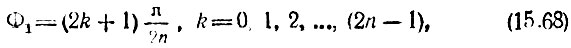
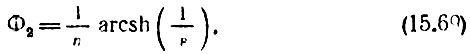
Для n плюсов, расположенных в левой р-полуплоскости, получается следующее выражение:

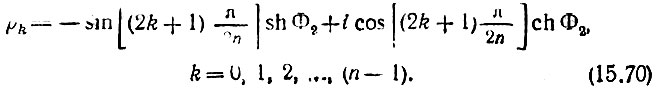
По найденным полюсам составляется выражение для передаточной функции К(р), аналогичное (15.59):

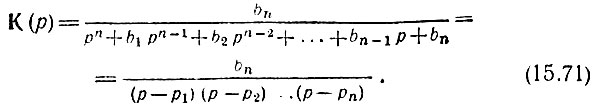
В отличие от фильтра Баттерворта коэффициент b_n не равен единице (поскольку полюса передаточной функции расположены не на окружности единичного радиуса, а на эллипсе). Поэтому в числитель вводится коэффициент b_n для нормирования АЧХ к единице при ω = 0 (и соответственно р = 0).

Численные значения коэффициентов b₁, b₂, ..., b_n, а также полюсов p₁, р₂, ..., р_n в зависимости от степени n и коэффициента неравномерности АЧХ ε приводятся в литературе по расчету фильтров [7, 8, 12].

Для иллюстрации синтеза фильтра Чебышева определим схему и параметры фильтра при следующих требованиях: неравномерность в полосе прозрачности не более 3 дБ, затухание при х = ω/ω_с = 4 не менее 30 дБ. При заданной неравномерности, приравнивая в выражении (15.64) А К величине 1/2, получаем ε = 1. Применяя далее формулу (15.65), находим требуемую величину

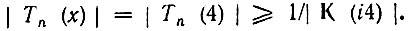
Ослаблению на 30 дБ соответствует уменьшение АЧХ в 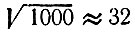раза. При максимальном значении АЧХ, равном единице, получаем следующее условие для определения порядка полинома Чебышева: Т_n(4) ≥ 1/32. Перебором первых трех полиномов низших степеней (см. § 14.2) убеждаемся, что полином второй степени при х = 4, равный T₂(4) = 2х² - 1 = 31, обеспечивает требуемую скорость убывания АЧХ в зоне задерживания. Применяя формулы (15.68), (15.70), находим

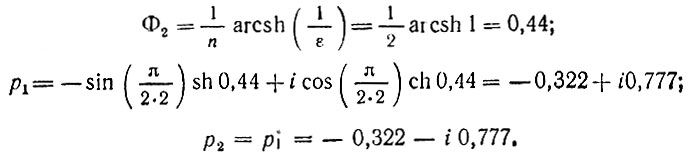
Передаточная функция (по формуле (15.71))

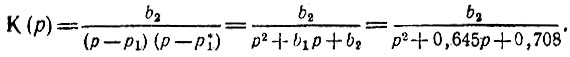
Приравнивая (как и в предыдущем параграфе) коэффициенты полинома в знаменателе выражения (15.61) соответственно b₁ = 0,645 и b₂ = 0,708, получаем следующие соотношения для определения параметров активной RС-цепи:

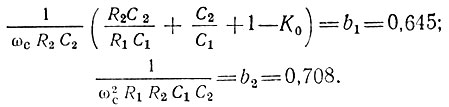
Сохранив соотношения, принятые в § 15.8 для фильтра Баттерворта 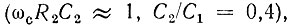получим

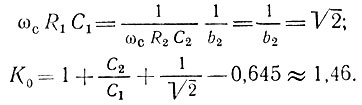
Из сопоставления полученных результатов с результатами расчета фильтра Баттерворта видим, что, изменяя коэффициент усиления К₀ (операционного усилителя) и несущественно изменяя сопротивления резисторов R₁, R₂ (или емкостей конденсаторов С₁, С₂), можно перейти от фильтра Баттерворта к фильтру Чебышева. Следует, однако, отметить, что при n = 2 фильтр Баттерворта обеспечивает ослабление АЧХ при х = ω/ω_с = 4 всего лишь на 24 дБ [см. формулу (15.52) при n = 2 и у = 2]. Для получения ослабления на 30 дБ потребовалось бы n ≥ 3 (одно звено второго порядка и одно апериодическое звено). Это преимущество фильтра Чебышева в зоне задерживания (более быстрое убывание АЧХ) достигается ценой некоторого ухудшения равномерности в полосе прозрачности фильтра.