15.10. Синтез различных фильтров на основе исходного фильтра нижних частот

Вернемся к функции (15.50), аппроксимирующей прямоугольную амплитудно-частотную характеристику идеального фильтра нижних частот, и введем новую переменную

Тогда

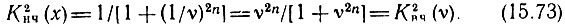
Новая функция К_вч(ν), получаемая из АЧХ К_нч(х) фильтра нижних частот заменой аргумента на ν = 1/x, показана на рис. 15.18 (для n = 2). Функцию К_вч можно рассматривать как АЧХ фильтра Баттерворта верхних частот, обладающего в полосе частот 1 < ν < ∞ такой же степенью неравномерности АЧХ, что и функция К_нч(х) в полосе 0 < х < 1. Таким образом, при синтезе фильтра верхних частот можно использовать аппроксимирующую функцию F(х) [см. (15.49)], заменив в ней аргумент на ν = 1/х.

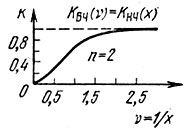
Рис. 15.18 Фильтр верхних частот Баттерворта

В соответствии о такой заменой, частотную переменную р в (15.58) следует заменить переменной s = 1/р. Функция (15.58) при этом принимает вид

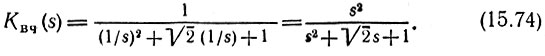
Полюса передаточной функции К_вч(s), т. е. корни уравнения 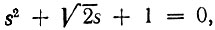остаются теми же, что и в (15.58).

Аналогичным образом можно получить передаточную функцию фильтра верхних частот Чебышева.

Соотношение между АЧХ фильтров Чебышева верхних и нижних частот представлено на рис. 15.19 (для n = 4).

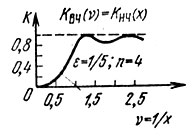
Рис. 15.19. Фильтр верхних частот Чебышева

Соответствующим преобразованием переменной р можно синтезировать и иные фильтры, например полосовые, на основе исходного фильтра нижних частот [7, 8, 12].