15.11. Чувствительность характеристик цепи к изменениям параметров элементов

В гл. 5 кратко рассматривалось влияние изменения коэффициента усиления прямой цепи К_у, а также модуля К_ос передаточной функции цепи обратной связи на усиление устройства в целом. Вопрос о запасе устойчивости четырехполюсника с обратной связью не рассматривался. Этот вопрос приобрел особенную актуальность при синтезе активных RC-цепей (и интегральных систем), в которых приходится считаться с относительно большой нестабильностью параметров активных элементов, зависимостью их от режима работы (изменения напряжений источников питания), температурных изменений и т. д. Необходимо также учитывать разброс параметров элементов; резисторов, конденсаторов и особенно активных элементов (транзисторов различного типа и других приборов современной микроэлектронной техники).

Передаточная функция линейной цепи однозначно определяется своими полюсами и нулями на р-плоскости. Поэтому различные дестабилизирующие факторы логично оценивать по величине создаваемого ими сдвига полюсов и нулей.

Особенно большое внимание приходится уделять сдвигу полюсов, так как именно положение полюсов определяет такие важные показатели цепи, как запас устойчивости, усиление, резонансная частота.

Большое распространение [12] получило математическое определение чувствительности параметра цепи W к изменению элемента X в виде уравнения

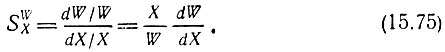
Символ W может иметь смысл коэффициента усиления K_у, добротности Q, корня р_k = σ_k + iω_k и. т. д., а X - сопротивления резистора, емкости конденсатора, какого-либо из параметров активного элемента (крутизны характеристики, внутренней проводимости и т. д.).

Применительно к оценке полюсной чувствительности выражение (15.75) часто записывается в следующей форме:

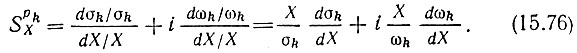
Первое слагаемое в правой части характеризует сдвиг полюса параллельно вещественной оси плоскости р = σ + iω, а второе - параллельно оси iω. Таким образом, первое слагаемое может служить оценкой запаса устойчивости цепи (поскольку приближение |σ_k| к нулю означает потерю устойчивости), а второе слагаемое характеризует изменение частоты, соответствующей пику амплитудно-частотной характеристики цепи.

Проиллюстрируем применение формулы (15.76) на примере передаточной функции К(р) фильтра Баттерворта, рассмотренного в § 15.8. Найдем чувствительность полюсов функции (15.61) к изменению величины К₀, рассматриваемой как параметр X в (15.76).

Подставив в (15.61) ω_cR₁С₂ = ω_cR₂C₁ = 1, C₁R₂/C₂R₁ = 1 и С₁/С₂ = 0,4 (см. конец § 15.8), получим

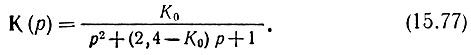
Полюса функции К(р)

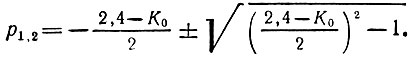
При К₀ < 0,4 корни вещественные, а при К₀ > 0,4 - комплексные.

В последнем случае

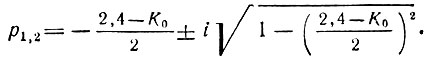
Как и в (15.61), имеется в виду нормированная переменная р = (σ + iω)/ω_c.

Модуль р_{1, 2} равен единице (при K₀ > 0,4), а вещественные и мнимые части соответственно

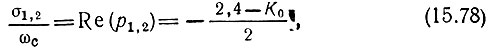
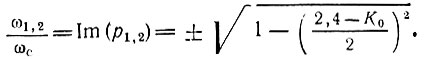
При увеличении K₀, начиная с K₀ = 0,4, полюса р_{1, 2} перемещаются по окружности единичного радиуса (рис. 15.20) (р₁ - по часовой стрелке, а р₂ - против). При K₀ = 2,4 коэффициент при р в знаменателе (15.77) обращается в нуль, что означает потерю устойчивости цепи.

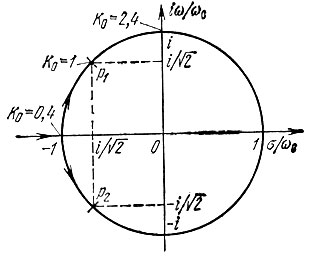
Рис. 15.20. Перемещение полюсов по окружности единичного радиуса при изменении К₀

Дифференцируя выражения (15.78) и подставляя производные

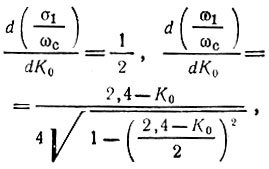
а также σ₁/ω_с и ω₁/ω_с в формулу (15.76) для k = 1, т. е. для корня р₁, получаем

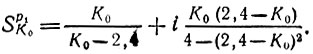
При исходном (расчетном) значении К₀ = 1

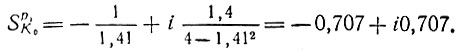
Однако при больших значениях К₀, например при К₀ = 2,

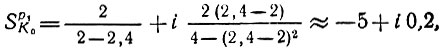
чувствительность абсциссы полюса достигает - 5, а ординаты уменьшается до 0,2.

По мере приближения К₀ к критическому значению, соответствующему возникновению генерации, чувствительность абсциссы полюса резко возрастает, а ординаты уменьшается.

Перераспределение емкостей С₁ и С₂ (уменьшением С₁ и увеличением С₂), что потребует увеличения К₀, можно добиться требуемой формы амплитудно-частотной характеристики при одновременном увеличении усиления в фильтре [поскольку в (15.61) коэффициент К₀ является числителем]. Однако при этом повышается чувствительность полюсов передаточной функции к изменению величины К₀.