3.4. Частотный метод радиодальнометрии

Принцип действия частотного радиодальномера, упрощенная блок-схема которого представлена на рис. 3.3, сводится к следующему.

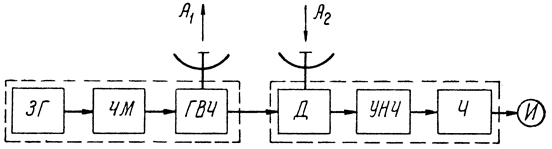
Рис. 3.3. Блок-схема частотного радиодальномера: А₁ - передающая антенна, ГВЧ - генератор высокой частоты, ЧМ - частотный модулятор, ЗГ - звуковой генератор, А₂ - приемная антенна, Д - детектор, УНЧ - усилитель низкой частоты, Ч - частотомер

От генератора высокой частоты на вход детектора поступает частотно-модулированное напряжение прямого сигнала u₁ (рис. 3.4, а). Одновременно на вход детектора от приемной антенны поступает напряжение отраженного сигнала u₂ (рис. 3.4, б).

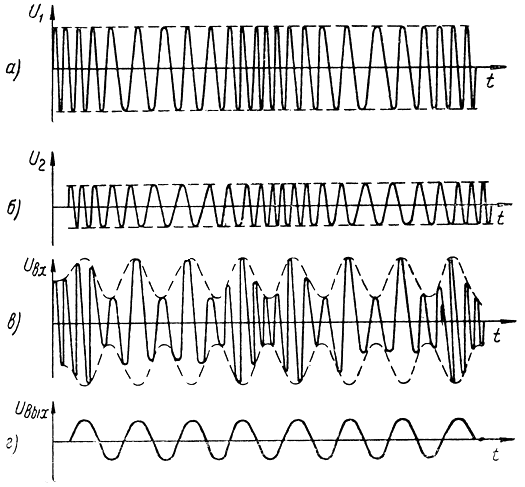
Рис. 3.4. Графики напряжений, поясняющие работу частотного радиодальномера: а - излучаемые частотно-модулированные колебания; б - принимаемые частотно-модулированные колебания; в - результирующее напряжение на входе приемника; г - напряжение на выходе детектора

Если расстояние до отражающей цели и эффективная площадь рассеяния последней с течением времени не меняются, то дополнительной модуляции колебаний при отражении не будет. В этих условиях отраженный сигнал будет отличаться от прямого только по амплитуде и запаздывать по времени на величину

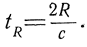
При сложении прямого и отраженного сигналов возникают биения, и результирующий сигнал оказывается модулированным как по частоте, так и по амплитуде (рис. 3.4, в). Число максимумов огибающей результирующего колебания в единицу времени зависит от величины временного сдвига, т. е. от расстояния до отражающей цели.

Если теперь путем детектирования результирующего сигнала выделить огибающую (рис. 3.4, г) и после необходимого усиления подать ее на частотомер, то показания частотомера будут функционально связаны с измеряемым расстоянием.

Следовательно, частотомер можно проградуировать в единицах расстояния.

Рассмотрим теперь основные соотношения.

Частотно-модулированные напряжения прямого и отраженного сигналов можно представить в следующем виде:

где U_m1 и U_m2 - амплитуды напряжений прямого и отраженного сигналов,

φ₁ и φ₂ - фазы прямого и отраженного сигналов.

Результирующий сигнал на входе детектора равен сумме прямого и отраженного сигналов. Поэтому напряжение результирующего сигнала будет

где U_m - амплитуда результирующего напряжения,

φ - фаза результирующего напряжения.

Амплитуда результирующего напряжения согласно векторной диаграмме, представленной на рис. 3.5, будет

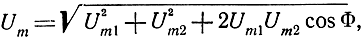
где

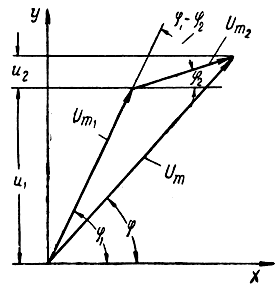
Рис. 3.5. Векторная диаграмма входного напряжения

Так как обычно U_m1 >> U_m2,

то

Фаза результирующего сигнала согласно той же диаграмме будет

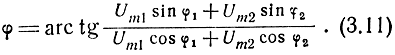
Из формулы (3.10) видно, что закон изменения огибающей результирующего сигнала определяется законом изменения разности фаз прямого и отраженного сигналов, который, в свою очередь, определяется законами изменения фаз каждого из сигналов.

Фаза прямого сигнала зависит только от закона изменения частоты излучаемых колебаний. Фаза отраженного сигнала зависит как от закона изменения частоты излучаемых колебаний, так и от закона движения объекта и величины сдвига фазы, возникающего при отражении.

Допустим, что частота прямого сигнала монотонно возрастает линейному закону (рис. 3.6), т. е.

где f₁ - мгновенная частота прямого сигнала,

f_н - начальное значение частоты,

а - скорость изменения частоты.

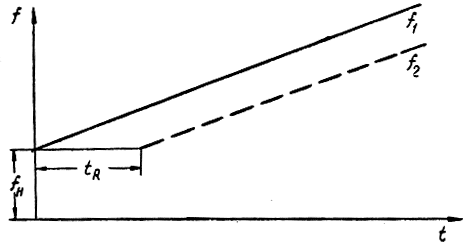
Рис. 3.6. Линейный закон изменения частоты

Тогда фаза прямого сигнала будет

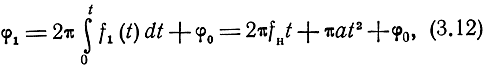
где φ₀ - начальная фаза прямого сигнала.

Фаза отраженного сигнала при неизменном расстоянии между дальномером и целью будет

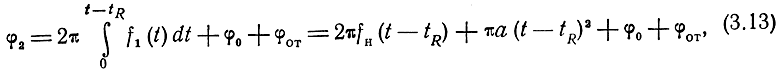
где φ_от - сдвиг фазы, возникающий при отражении.

Разность фаз прямого и отраженного сигналов будет

где Ф₀ = 2πf_нt_R - πat²_R - φ_от.

Как видим, разность фаз прямого и отраженного сигналов при φ_от = const является линейной функцией времени. Поэтому амплитуда результирующего сигнала согласно выражению (3.10) будет с течением времени меняться по гармоническому закону.

Другими словами, результирующий сигнал будет модулирован по амплитуде по гармоническому закону. Кроме того, результирующий сигнал будет модулирован и по частоте, в чем можно убедиться, если взять производную по времени выражения (3.11). Однако это не является существенным, поскольку после детектирования выделяется только огибающая результирующего сигнала. Сосредоточим поэтому все внимание на законе огибающей.

На рис. 3.7 представлена векторная диаграмма для случая, когда Ф₀ = n2π, где n - целое число. При возрастании времени разность фаз Ф согласно выражению (3.14) будет возрастать, в силу чего вектор отраженного сигнала U_m2 будет вращаться относительно точки О. В результате вектор результирующего сигнала U_m будет меняться в пределах от U_m = U_m1 + U_m2 до U_m = U_m1 - U_m2. Форма огибающей результирующего сигнала представлена на том же рис. 3.7.

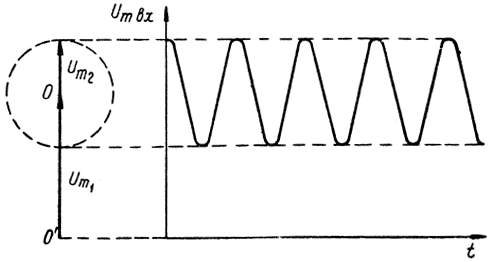
Рис. 3.7. Векторная диаграмма и форма огибающей результирующего сигнала

Скорость изменения разности фаз прямого и отраженного сигналов и угловая частота биений в рассматриваемом случае - понятия тождественные.

Поэтому угловая частота биений

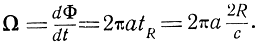
Частота биений

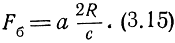
Закон изменения частоты отраженного сигнала при оговоренных ранее условиях

Разность мгновенных значений частот прямого и отраженного сигналов

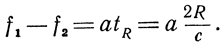
Как видим, частота биений

Таким образом, частота биений в рассматриваемом случае зависит линейно от измеряемого расстояния и равна разности мгновенных значений частот прямого и отраженного сигналов. Не следует упускать из виду, что полученные соотношения справедливы только для случая, когда частота излучаемых колебаний меняется по линейному закону. Однако обеспечить равномерное изменение частоты передатчика в сторону повышения или понижения ее в течение продолжительного времени невозможно. Это обстоятельство заставляет прибегать к периодическому изменению частоты.

В современных частотных радиодальномерах наибольшее распространение получила модуляция по закону симметричной треугольной кривой (рис. 3.8) и по гармоническому закону (рис. 3.9).

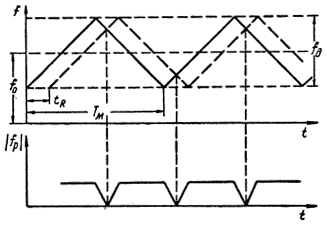
Рис. 3.8. Зависимость модуля разности частот прямого и отраженного сигналов от времени при модуляции по закону симметричной треугольной кривой

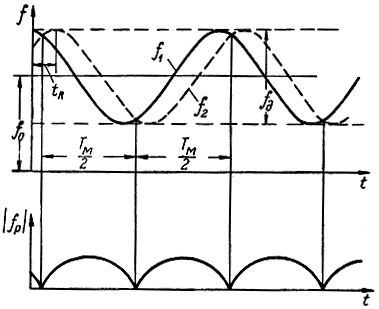
Рис. 3.9. Зависимость модуля разности частот прямого и отраженного сигналов от времени при модуляции по гармоническому закону

Из рис 3.8 видно, что при t_R << T_м в течение большей части времени модуль разности частот прямого и отраженного сигналов будет

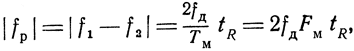
где f_д - пределы отклонения частоты (девиация частоты),

Т_м - период модуляции,

F_M - частота модуляции.

Если |f_р| >> F_M, то, как и ранее, можно считать, что

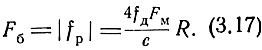
При модуляции по гармоническому закону (рис. 3.9) частота прямого сигнала будет

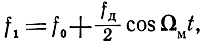
где f₀ - среднее значение частоты,

Ω_M = 2πF_M - угловая частота модуляции.

Частота отраженного сигнала будет

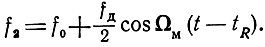
Модуль разности частот прямого и отраженного сигналов

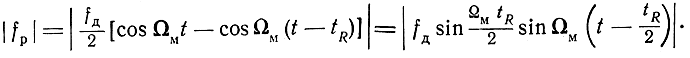
Если 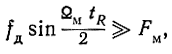то можно считать, что для большей части периода модуляции

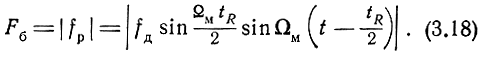
Как видим, при модуляции по гармоническому закону частота биений при неизменном расстоянии периодически меняется.

Однако показания частотомера при достаточной инерционности его будут соответствовать средней частоте биений, равной

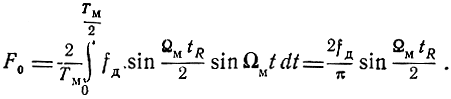
Учитывая, что обычно t_R << T_M, можно считать

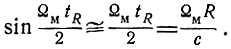
Тогда

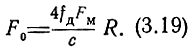
Следует, однако, иметь в виду, что равенства (3.17) и (3.18) в отличие от выражения (3.16) являются приближенными, так как в силу периодического изменения частоты излучаемых колебаний средняя частота биений не может плавно изменяться с изменением расстояния, а может принимать лишь дискретные значения, кратные частоте модуляции.

Для подтверждения сказанного рассмотрим подробнее основные соотношения при гармонической модуляции.

Фаза прямого сигнала в этом случае будет

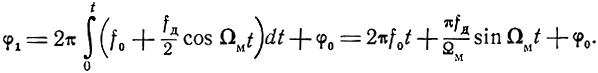
Фаза отраженного сигнала без учета сдвига фазы, возникающего при отражении, будет

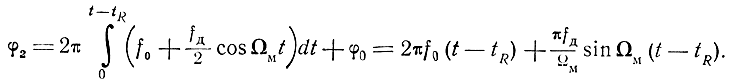
Разность фаз прямого и отраженного сигналов будет

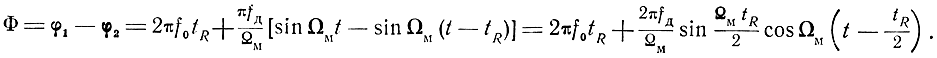
Обозначим среднюю разность фаз через

и амплитуду разности фаз через

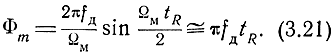
Тогда

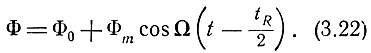
Из полученного выражения видно, что разность фаз прямого и отраженного сигналов является гармонической функцией времени (рис. 3.10) с периодом, равным периоду модуляции. Поэтому результирующий сигнал будет модулирован по амплитуде.

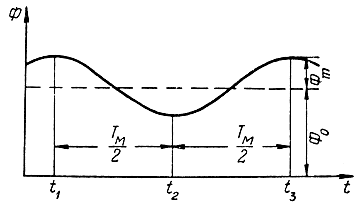
Рис. 3.10. Зависимость разности фаз прямого и отраженного сигналов от времени при гармоническом законе изменения частоты

Если

то на половине периода модуляции уложится ряд периодов биений. В этих условиях выражение (3.19) будет справедливо, хотя и приближенно.

На рис. 3.11 представлена векторная диаграмма для момента времени t₁ (рис. 3.10), когда разность фаз Ф максимальна. При возрастании t от t₁ до t₂ разность фаз Ф будет уменьшаться, в силу чего вектор отраженного сигнала U_m2 будет вращаться относительно точки 0. При этом результирующий вектор будет меняться в пределах от U_m1 + U_m2 до U_m1 - U_m2.

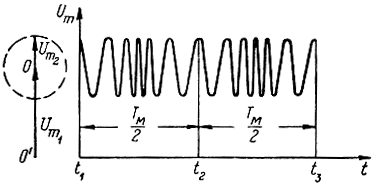
Рис. 3.11. Векторная диаграмма и форма огибающей результирующего сигнала при Ф₀ = n2π и Ф_m = 6π

При дальнейшем возрастании t от t₂ до t₃ разность фаз будет возрастать, поэтому вектор U_m2 будет вращаться в противоположном направлении. Затем в следующие периоды модуляции вся картина будет повторяться.

На том же рис. 3.11 представлена форма огибающей результирующего сигнала для случая, когда

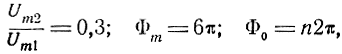
где n - целое число.

Как видим, при изменении разности фаз прямого и отраженного сигналов на величину, равную 2π, происходит полный цикл изменения огибающей результирующего сигнала.

Так как полное изменение разности фаз Ф от Ф_макс до Ф_мин происходит за время, равное половине периода модуляции, то число полных циклов биений N за то же время будет равно целой части отношения

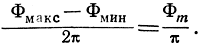
Подставляя значение Ф_m из формулы (3.21) и считая, что при Ф_m >> 2π целая часть отношения 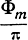мало отличается от отношения 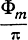, получаем

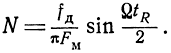
Поскольку скорость изменения разности фаз прямого и отраженного сигналов в пределах полупериода модуляции не остается постоянной, то периоды биений не будут равны между собой, т. е. частота биений в пределах полупериода модуляции будет меняться. Однако показания частотомера в силу его инерционных свойств будут соответствовать средней частоте биений, равной

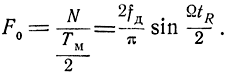
При t_R << T_M

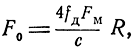
что полностью совпадает с ранее полученным выражением (3.19). Разумеется, что число максимумов огибающей за полпериода модуляции может быть только целым. Поэтому средняя частота биений не может плавно изменяться с изменением расстояния, а может принимать лишь дискретные значения, кратные частоте модуляции.

Сказанное легче всего проиллюстрировать на примере измерений малых расстояний, когда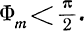

Пусть средняя разность фаз

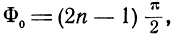
где n - целое число.

Векторная диаграмма и форма огибающей, соответствующие этому случаю, представлены на рис. 3.12.

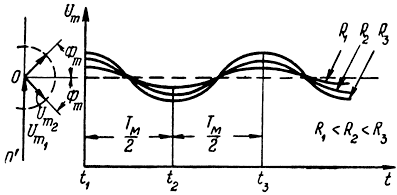
Рис. 3.12. Векторная диаграмма и форма огибающей результирующего сигнала при

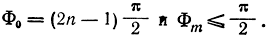
При возрастании R будут возрастать как Ф₀, так и Ф_m. Однако, как следует из выражений (3.20) и (3.21), Ф₀ возрастает в 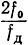раз быстрее, чем Ф_m. Поэтому имеется ряд различных значений R, для которых условия 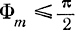и 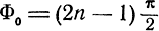выполняются.

На рис. 3.12 представлен ряд огибающих результирующего сигнала, соответствующих этим значениям R.

Легко видеть, что, пока Ф_m ≤ ^π/₂, число периодов биений за один период модуляции при различных значениях R остается неизменным. Меняется лишь глубина амплитудной модуляции результирующего сигнала. Минимальная частота биений в рассматриваемом случае будет

Подставив это значение F_{б мин} в выражение (3.19) и решив его относительно R, найдем минимальные показания радиодальномера (не считая, конечно, нуля), т. е. первую отсчетную точку

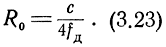
Пусть теперь Ф₀ = nπ, а Ф_m ≤ π.

Векторная диаграмма и форма огибающей, соответствующие этому случаю, представлены на рис. 3.13.

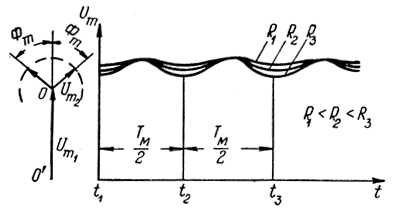
Рис. 3.13. Векторная диаграмма и форма огибающей результирующего сигнала при Ф₀ = nπ и Ф_m ≤ π

Здесь также имеется ряд значений R, для которых оговоренные условия выполняются.

Легко видеть, что, пока Ф_m ≤ π, число периодов биений за один период модуляции при изменении R остается постоянным. Меняется лишь глубина амплитудной модуляции, результирующего сигнала. Минимальная частота биений в рассматриваемом случае будет

а следовательно, минимальное измеряемое расстояние будет

Итак, при измерении малых расстояний показания радиодальномера не будут совпадать с истинным значением R и, в зависимости от величины Ф₀, могут иметь только одно из двух значений: либо R₀, либо 2R₀. Других показаний быть не может.

Как же будут меняться показания радиодальномера при плавном возрастании расстояния начиная от нуля?

Поскольку при возрастании расстояния Ф₀ будет возрастать быстрее, чем Ф_m в 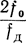раз, то будет быстрее изменяться взаимное расположение векторов U_m1 и U_m2 на рис. 3.12 или 3.13, по сравнению с изменением угла размаха колебаний вектора U_m2. Поэтому, пока расстояние возрастает от 0 до 2R₀, показания радиодальномера несколько раз скачком изменятся между значениями R₀ и 2R₀.

При дальнейшем увеличении расстояния показания радиодальномера будут несколько раз изменяться между значениями 2R₀ и 3R₀, затем между 3R₀ и 4R₀ и т. д.

Характер зависимости показаний радиодальномера от расстояния представлен на рис. 3.14.

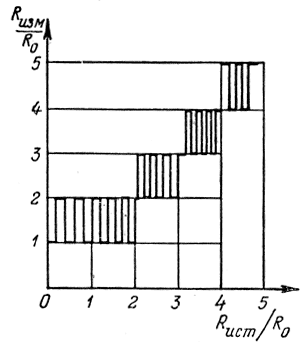
Рис. 3.14. Зависимость показаний частотного радиодальномера от расстояния

Таким образом, показания радиодальномера не могут точно следовать за изменением расстояния, а могут принимать лишь ряд дискретных значений, кратных R₀. Следовательно, выражения (3.17) и (3.19) являются приближенными.