1. Передаточные и переходные функции систем автоматического управления

Передаточные и переходные функции системы являются характеристиками, которые позволяют по известной функции на входе системы определить функцию на выходе системы.

При этом, если напряжения на входе и выходе системы являются функциями времени (t), то система характеризуется переходной функцией. Если же эти напряжения зависят от комплексной частоты (s), то система определяется передаточной функцией. Рассмотрим эти функции и методику их определения.

Напомним, что преобразованной по Лапласу или лапласовым изображением функции времени [u(t)] называется функция [U(s)], определяемая следующим образом:

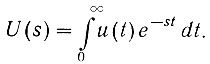(4.3)

Благодаря преобразованию Лапласа вместо времени (t) переменной величиной становится комплексная частота

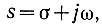(4.4)

где σ - действительная часть комплексной частоты;

ω - мнимая часть этой частоты.

Обратное преобразование выполняется решением уравнения (4.3) относительно u(t):

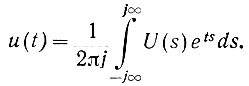(4.5)

Преобразование Лапласа делает возможным анализ характеристик систем автоматического управления на основе хорошо развитой теории функции комплексного переменного. Благодаря этому операции дифференцирования заменяются умножением на комплексную частоту:

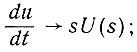(4.6)

дифференциальные уравнения превращаются в алгебраические, что резко упрощает решение различных задач.

Пример. Определить кривую тока, получающегося в схеме рис. 4.1 после включения контактора (R и L - постоянные величины).

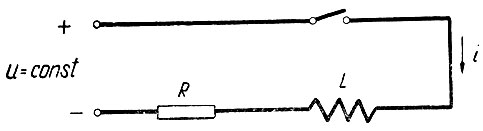
Рис. 4.1. Схема цепи с комплексным сопротивлением

Для этой цепи можно записать следующую зависимость:

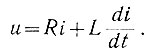
Чтобы найти ток, нужно решить это дифференциальное уравнение. Если же уравнение записать не для тока i и напряжения u, а для их лапласовых изображений [I(s) и U(s)], то получим

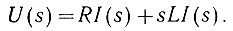
Это уравнение уже является не дифференциальным, а алгебраическим. Поэтому искомый ток (его изображение) определяется как частное

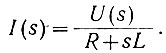
Поскольку напряжение и является постоянной величиной, его изображение равно

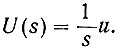
Следовательно,

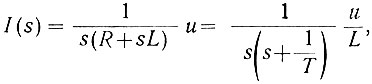
где 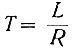- постоянная времени схемы.

Определяя по таблицам преобразованных (по Лапласу) функций исходную функцию, получаем

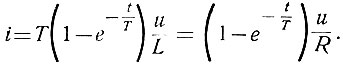
Статистическая теория требует рассмотрения всего диапазона изменения функции u(t) от t = -∞ до t = ∞. В этом случае для определения преобразованной функции используют двухстороннее преобразование Лапласа, которое в отличие от обычного (ур. 4.3) определяется уравнением

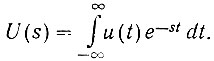(4.7)

Запишем правую часть этого уравнения в виде суммы двух составляющих:

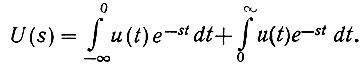
В первом интеграле заменим переменную t на τ = -t; тогда получим

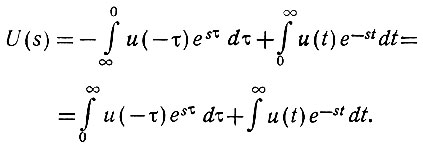
Далее для первого интеграла введем новую переменную в комплексной области: s' = -s. В этом случае

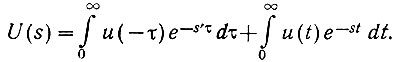
Следовательно, нахождение двухстороннего изображения Лапласа функции u(t), существующей при ∞ > t > -∞, распадается на две части.

Прежде всего (правый интеграл ур. 4.8) необходимо определить обычное изображение Лапласа от функции u(t), существующей при t > 0 (ур. 4.3).

Затем (левый интеграл ур. 4.8) определяется обычное изображение Лапласа, но не функции u(t), а ее зеркального отображения (рис. 4.2) и в полученном изображении меняется знак комплексной частоты.

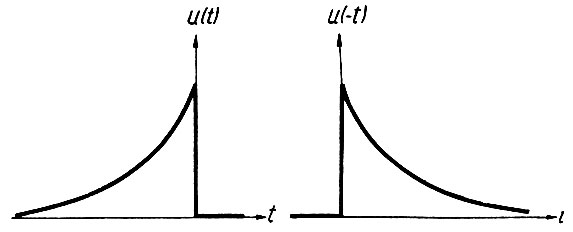
Рис. 4.2. Зеркальное отображение функции (справа) по первоначальной (слева)

Сумма этих составляющих и дает двухстороннее преобразование Лапласа от функции u(t).

Пример. Определить двухстороннее изображение Лапласа функции

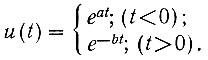
Вначале определяем обычное изображение Лапласа для функции e^-bt, существующей при t > 0. Пользуясь таблицами преобразованных функций, получаем

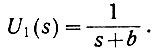
Вторую составляющую изображения находим следующим образом:

а) меняем в u(t) знак перед t на обратный (находим зеркальное отображение функции u(t) при t < 0):

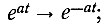
б) находим обычное изображение Лапласа для зеркального отображения функции:

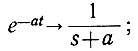
в) меняем знак комплексной частоты и получаем

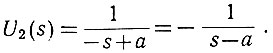
Следовательно, двухстороннее изображение Лапласа равно

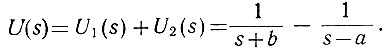
В области комплексного переменного (s) система автоматического управления характеризуется передаточной функцией, представляющей собой отношение изображения Лапласа выходной функции системы к изображению Лапласа входной функции при нулевых начальных условиях:

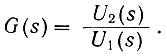(4.10)

Следует отметить, что эта характеристика не зависит от формы сигнала на входе системы и поэтому может быть применена в статистических расчетах.

Передаточная функция зависит от комплексной частоты (s = σ + jω) и изображается плоской кривой в координатах: σ (действительная ось) и jω (мнимая ось).

Если в уравнении (4.9) принять s = jω, то получим амплитудо-фазовую характеристику системы:

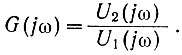(4.10)

Замена комплексной частоты s мнимой jω равносильна (ур. 4.4) приравниванию нулю действительной составляющей частоты σ. Следовательно, амплитудо-фазовая характеристика является частным случаем передаточной функции и показывает ее изменение по оси мнимых частот (σ = 0). Называется эта характеристика "амплитудо-фазовой" потому, что при подаче на вход системы синусоидального сигнала она позволяет определить амплитуду и фазу напряжения на выходе системы.

Если задана амплитудо-фазовая характеристика, то, заменив в ней jω на s, можно получить передаточную функцию.

Амплитудо-фазовая характеристика может быть записана в несколько ином виде:

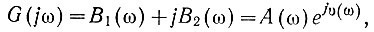(4.11)

где

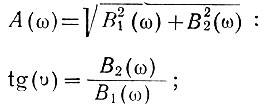
B₁(ω) и B₂(ω) - действительная и мнимая составляющие амплитудо-фазовой характеристики.

Величину A(ω) часто называют амплитудной частотной характеристикой, а υ(ω) - фазовой частотной характеристикой.

Рассмотрим пример определения передаточной и амплитудо-фазовой характеристик.

Необходимо определить передаточную характеристику для генератора постоянного тока (рис. 4.3).

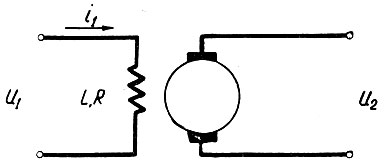
Рис. 4.3. Схема генератора постоянного тока

Для цепи обмотки возбуждения этого генератора можно записать:

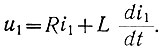
Поэтому, переходя к изображениям Лапласа, получаем

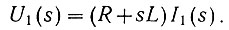
Пренебрегая насыщением магнитной цепи генератора, можно записать, что

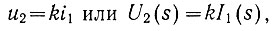
где k - коэффициент пропорциональности.

Тогда

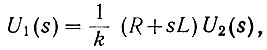(4.12)

откуда определяется передаточная функция

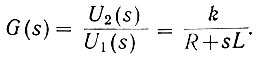(4.13)

Полагая s = jω, определяем амплитудо-фазовую характеристику:

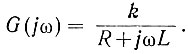
Это выражение (ур. 4.11) может быть легко преобразовано и записано в виде

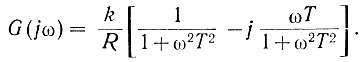
Как следует из рис. 4.4, эта функция является полуокружностью с центром в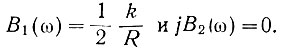

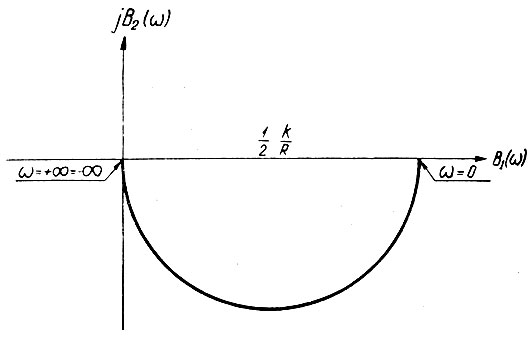
Рис. 4.4. Амплитудо-фазовая характеристика

Если система автоматического управления замкнута (рис. 4.5), то для нее можно записать:

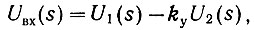
где k_y - передаточный коэффициент цепи обратной связи.

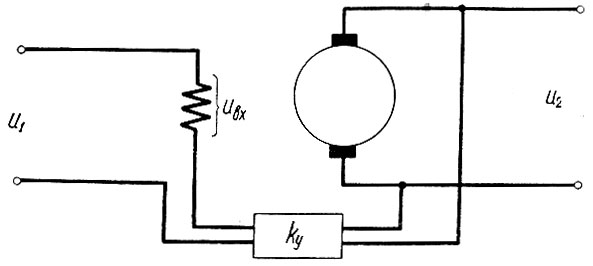
Рис. 4.5. Схема замкнутой системы автоматического управления

Нетрудно заметить, что u_вх играет здесь ту же роль, что u₁ в схеме рис. 4.3. Поэтому (ур. 4.12)

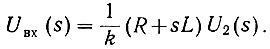
Решая совместно оба последних уравнения, получаем

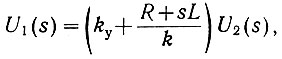
откуда легко определить передаточную функцию замкнутой системы автоматического управления:

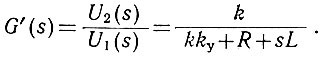
В общем виде передаточную функцию замкнутой системы автоматического управления можно определить, если в полученное уравнение подставить

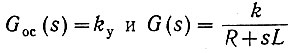
(ур. 4.13); в итоге получаем

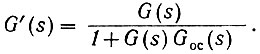(4.14)

где G_oc(s) - передаточная функция обратной связи.

Следует, иметь в виду, что все системы автоматического управления, за исключением программных, являются замкнутыми и, следовательно, имеют одну или несколько цепей обратной связи.

В большинстве случаев исследование систем автоматического управления производится в области комплексного переменного. Однако в ряде случаев это исследование удобно проводить не в комплексной области, а в плоскости вещественной переменной t. Рассмотрим поэтому, какие зависимости определяют систему во временной области.

Пользуясь уравнением (4.5), найдем обратное преобразование Лапласа для передаточной функции:

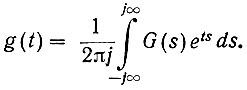(4.15)

Связь между g(t) и G(s) может быть также (ур. 4.3) записана в следующем виде:

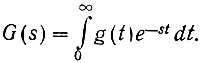(4.16)

Величину g(t) принято называть импульсной переходной функцией системы. Как следует из уравнений (4.15) и (4.16), импульсная переходная и передаточная функции взаимно связаны преобразованием Лапласа:

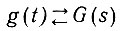
и характеризуют систему соответственно во временной и частотной областях.

Напряжение на выходе системы может быть определено по его изображению Лапласа (ур. 4.5):

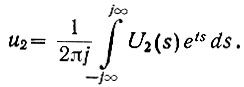
Поскольку (ур. 4.9)

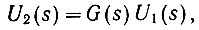
то

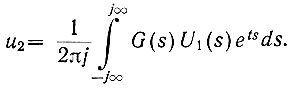
Для частного случая, когда U₁(s) = 1, имеем

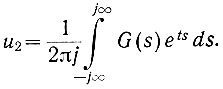(4.17)

Сравнивая уравнения (4.15) и (4.17), можно сделать следующий вывод: импульсная переходная функция системы [g(t)] равна напряжению на выходе системы (u₂), когда на вход системы подано напряжение, лапласово изображение которого равно единице.

Опуская доказательство, отметим, что функцией, лапласово изображение которой равно единице, является так называемая импульсная или дельта-функция.

Таким образом, импульсная переходная функция системы автоматического управления [g(t)] равна напряжению на выходе системы при подаче на ее вход импульсной функции [δ(t)].

Импульсная функция характерна тем, что в момент t = 0 она равна бесконечности, а в остальное время - нулю:

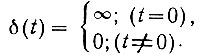(4.18)

Кроме того, площадь, описываемая импульсной функцией, равна

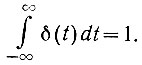
Следует иметь в виду, что в теории автоматического управления часто используют так называемую единичную функцию. Это функция (рис. 4.6), которая равна единице при t > 0 и нулю - при t < 0:

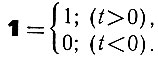(4.19)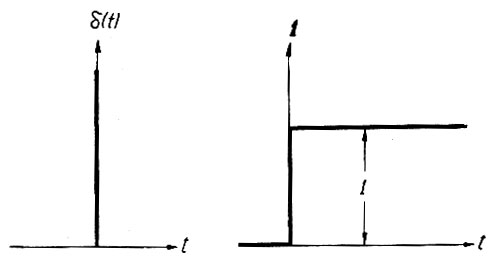

Рис. 4.6. Импульсная (слева) и единичная (справа) функции

Связь между единичной и импульсной функциями легко установить, взяв производную единичной функции:

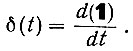(4.20)

Выше было показано, что импульсная переходная функция [g(t)] равна напряжению на выходе системы при подаче на ее вход импульсной функции. Аналогично этому в теории автоматического управления часто используется единичная переходная функция [h(t)], которая равна напряжению на выходе системы при подаче на ее вход единичной функции. Как следует из уравнения (4.20), эти виды переходных функций связаны между собой зависимостью

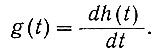
Итак, при подаче на вход системы импульсной функции на ее выходе появляется напряжение, равное g(t). Что же произойдет в том случае, когда на вход системы будет подано напряжение произвольной формы?

Определим вначале двухстороннее преобразование Лапласа для произвольной функции u₁(t), поданной на вход системы. Как следует из уравнения (4.7), это преобразование равно

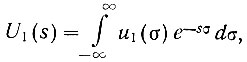(4.21a)

где σ - вещественная переменная времени, введенная в связи с тем, что в дальнейшем понадобится несколько переменных времени.

Кроме того (ур. 4.16), двухстороннее преобразование Лапласа для импульсной переходной функции равно

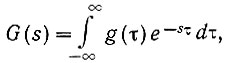(4.21б)

где τ - вторая вещественная переменная времени.

Подставив значения U₁(s) и G(s) в уравнение (4.9), определим преобразование Лапласа для функции, получающейся на выходе системы:

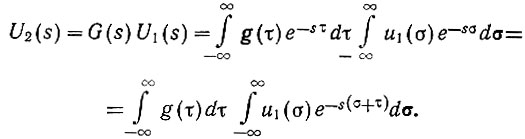
Введем для правого интеграла новую переменную времени

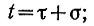
тогда

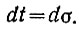
В этом случае получим

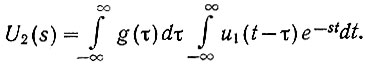
Изменим порядок интегрирования этого уравнения и запишем:

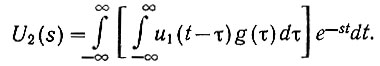
Сравнивая это уравнение с уравнением (4.7), получаем

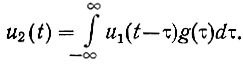(4.22)

Этот интеграл означает следующее. Непрерывно изменяющаяся функция на входе системы [u₁(t)] делится на бесконечно большое число импульсов, а интеграл осуществляет суммирование сигналов на выходе системы, получающихся при подаче на ее вход этих импульсов.

Поэтому интеграл (ур. 4.22) называется интегралом свертки.

Как было показано ранее (ур. 4.9), в области комплексной частоты напряжение на выходе определялось умножением входной функции на передаточную:

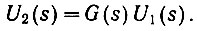
Во временной области это напряжение определяется интегралом свертки. Поэтому говорят, что умножение в частотной области эквивалентно свертке во временной области.

Следует иметь в виду, что τ, входящая в интеграл свертки, как и t, обозначает время. Однако, если t - время, в зависимости от которого изменяется функция u₁(t), то τ - время, характеризующее сдвиг относительно оси ординат каждого из бесконечного числа импульсов, из которых состоит эта функция. При вычислении интеграла свертки переменной является τ, а время t остается неизменным, ибо интегрирование осуществляется суммированием импульсов по τ.