2. Корреляционные функции

Ранее уже говорилось о том, что в большинстве случаев целью статистического расчета является сведение к минимуму среднеквадратичной ошибки (ур. 4.1).

Подставим в уравнение (4.1) значение функции на выходе системы (ур. 4.22). Тогда получим:

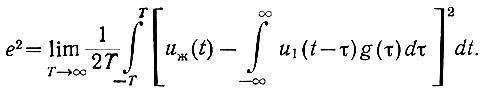
Возведем в квадрат выражение, заключенное в квадратные скобки:

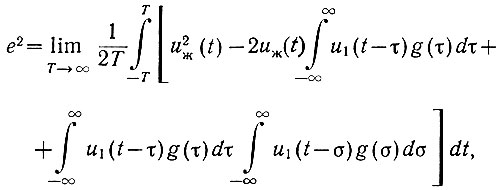
где σ - новая переменная времени, введенная для отличия от τ.

Следовательно, среднеквадратичная ошибка может быть представлена при помощи трех членов:

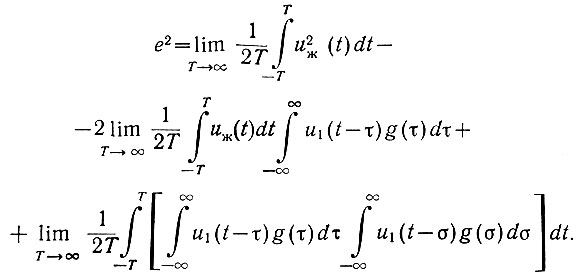
Поменяем местами во втором и третьем членах операции предельного перехода и интегрирования. Тогда получим

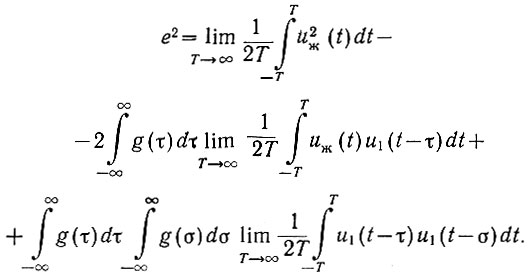(4.23)

Введем следующие обозначения:

а) автокорреляционную функцию входного сигнала

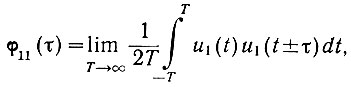(4.24)

б) автокорреляционную функцию выходных (действительного и желаемого) сигналов

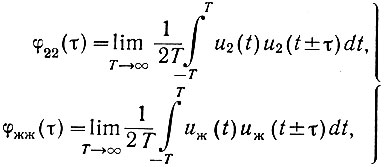(4.25)

в) взаимокорреляционную функцию входного и выходного сигналов

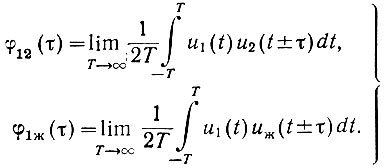(4.26)

Знак перед τ (в подынтегральном выражении) не имеет значения и может быть выбран любым (плюс или минус).

Легко увидеть, что корреляционная функция является средним по времени произведением двух функций, сдвинутых относительно друг друга на ±τ секунд.

Подставив значения корреляционных функций в уравнение (4.23), получим

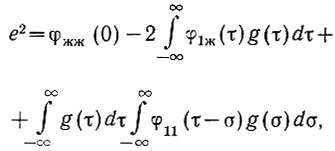(4.27)

где φ_жж(0) - автокорреляционная функция при τ = 0.

Таким образом, величина среднеквадратичной ошибки зависит от импульсной переходной и корреляционных функций.

Следует отметить, что в том случае, когда известна импульсная переходная функция, корреляционные функции могут быть выражены одна через другую. Рассмотрим эти зависимости. Если на вход системы подать напряжение произвольной формы, то напряжение на ее выходе (ур. 4.22) будет равно

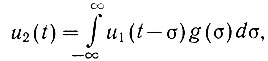
где σ и t - переменные времени.

Умножим обе части этого уравнения на u₁(t - τ):

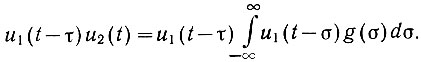
Проведем так называемое усреднение обеих частей уравнения, т. е. определим предел их интегралов:

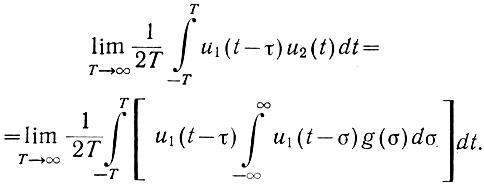
Левая часть этого уравнения равна (ур. 4.26) взаимокорреляционной функции. Поэтому, учитывая, что φ₂₁(τ) = φ₁₂(τ), последнее уравнение может быть записано в следующем виде:

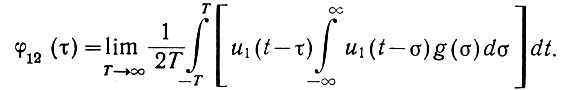
Меняя порядок интегрирования, получаем

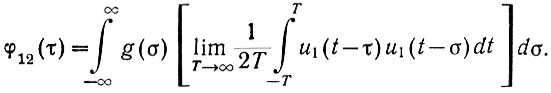
Выражение, стоящее в квадратных скобках (ур. 4.24), есть не что иное, как автокорреляционная функция с аргументом τ - σ. Поэтому

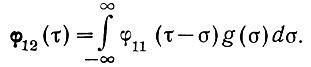
Поскольку в этом уравнении имеется всего две переменных времени, то можно вместо а взять более привычную переменную - t:

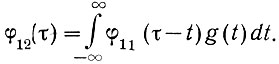(4.28)

Таким образом, зная импульсную переходную функцию системы, можно по автокорреляционной функции входного сигнала найти взаимокорреляционную функцию.

Определим далее соотношение между автокорреляционными функциями входного и выходного сигналов системы.

Автокорреляционная функция выходного сигнала (ур. 4.25) равна

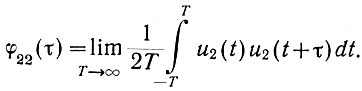
На основании уравнения (4.22) можно записать, что

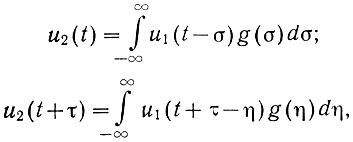
где σ и η - переменные времени.

Подставив значения функций u₂(t) и u₂(t + τ) в предыдущее уравнение, получим

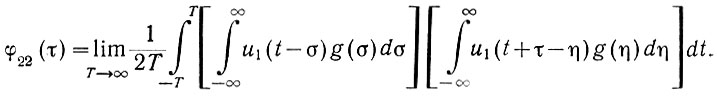
Меняя порядок интегрирования, записываем:

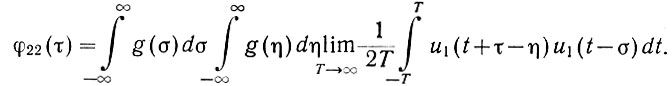
Поскольку (ур. 4.24)

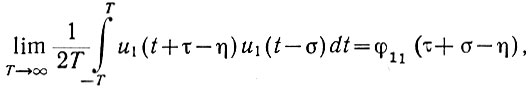
то

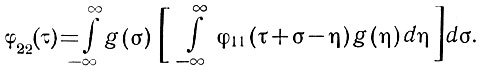(4.29)

Это выражение показывает связь между автокорреляционными функциями входа и выхода.

Рассмотрим некоторые свойства корреляционных функций.

а) Автокорреляционная функция при τ = 0 характеризует среднюю мощность функции. Действительно, пусть u(t) является напряжением, приложенным к сопротивлению 1 ом. Тогда автокорреляционная функция (ур. 4.24 или 4.25) выражает собой мощность на входе или на выходе системы.

б) |φ₁₁(τ)| ≤ φ₁₁(0). Докажем это неравенство. Произведение двух функций можно записать в следующем виде:

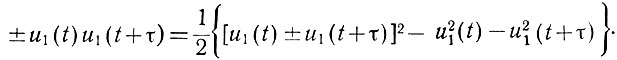
Осреднение обеих частей дает

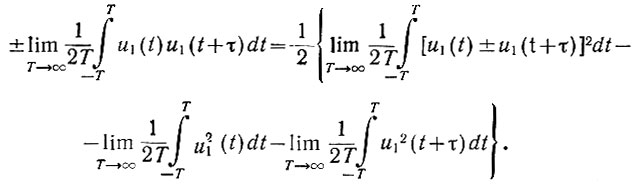
Поэтому, используя обозначения (4.24), запишем

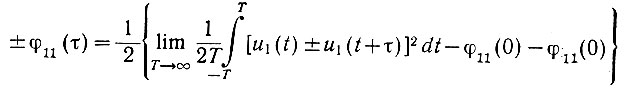
или

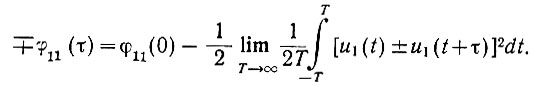
Поскольку второй член правой части всегда больше нуля (подынтегральный член возводится в квадрат), то абсолютное значение φ₁₁(τ) всегда меньше φ₁₁(0).

в) Если u(t) содержит периодическую или постоянную составляющую, то автокорреляционная функция также содержит периодическую или постоянную составляющую. Это следует из самого определения корреляционных функций.

г) Если u₁(t) является случайной функцией, то взаимокорреляционная функция φ₁₂(τ) → 0 при τ → ∞, ибо по мере увеличения τ функции u₁(t) и u₂(t) становятся независимыми друг от друга.

д) Данной автокорреляционной функции соответствует бесчисленное множество функций времени, но одной функции времени соответствует только одна автокорреляционная функция. Это происходит потому, что автокорреляционная функция является результатом осреднения функции времени.

Рассмотрим способ определения корреляционных функций при помощи вычислительных устройств. Схема одного из аппаратов, предназначенных для определения корреляционных функций, показана на рис. 4.7.

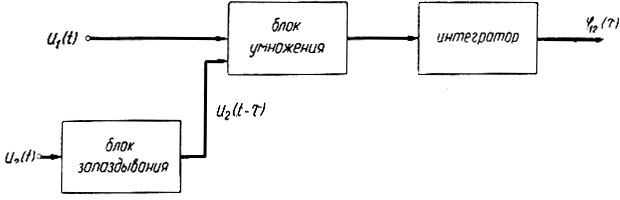
Рис. 4.7. Схема коррелятора

Эта схема выполнена на устройствах непрерывного действия и имеет два входа, на которые подаются напряжения на входе u₁(t) и выходе u₂(t) системы. Напряжение u₂(t) при помощи блока запаздывания сдвигается на τ сек. Простейшей схемой блока запаздывания является магнитофонная лента с двумя головками: записывающей и читающей. Если магнитная лента движется со скоростью то расстояние между головками определяется уравнением

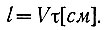
Перемножение функций u₁(t), u₂(t - τ) и интегрирование полученного произведения дает (ур. 4.26) искомую взаимокорреляционную функцию.

Если на оба входа схемы подать одно и то же напряжение, то на выходе получится автокорреляционная функция этого напряжения.

Естественно, что интегрирование в этом аппарате не может быть произведено при T → ∞. Поэтому в соответствии с законом больших чисел оно проводится в течение достаточно большого периода времени.

Блок умножения, используемый в этой схеме, должен обладать способностью пропускать высокие частоты. В противном случае он внесет большую ошибку в определение корреляционной функции.

Схема, аналогичная рис. 4.7, может быть создана и на основе дискретных вычислительных устройств, которые выполняют численное интегрирование произведения функций.

В случае, когда имеется математическое описание функций u₁(t) или u₂(t), соответствующие корреляционные функции могут быть также определены при помощи уравнений (4.24), (4.25) и (4.26).

Пример. Нужно определить автокорреляционную функцию для синусоиды

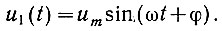
Согласно уравнению (4.24), записываем:

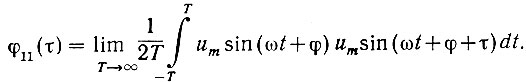
Так как здесь u₁(t) - периодическая функция, то интегрирование может быть выполнено в пределах одного периода (далее все будет повторяться):

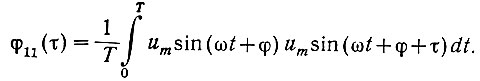
Поскольку u_m = const и 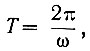то получаем

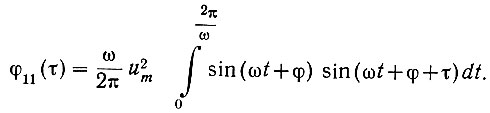
Обозначим ν = ωt + φ.

Тогда dν = ωdt и

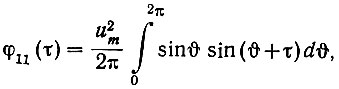
откуда после интегрирования получаем

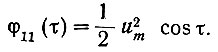(4.30)

Следовательно, автокорреляционной функцией синусоиды является косинусоида, не зависящая от начала отсчета времени (угла φ).

В последнее время разработан способ определения импульсной переходной характеристики системы g(t) при помощи шума. Шум, обычно являющийся помехой, в данном случае становится средством для определения характеристики системы. Ценность этого метода заключается в том, что импульсная переходная характеристика может быть определена без отключения системы во время ее нормальной работы. Проанализируем сущность этого метода.

Подадим на вход системы белый шум - абсолютно случайную функцию (напряжение), которая характеризуется тем, что в ней отсутствует какая-либо взаимная связь (корреляция) между предыдущими и последующими ее значениями. Поэтому для белого шума [ш₁(t)] автокорреляционная функция равна нулю при всех значениях τ, кроме точки τ = 0, где случайная функция умножается (ур. 4.24) сама на себя. Поэтому автокорреляционной функцией белого шума является импульсная функция.

Связь между функциями входа и выхода системы определяется уравнением (4.22):

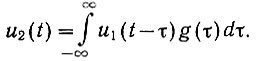(4.31а)

Если же для большей наглядности поменять местами в уравнении (4.28) переменные τ и t, то получим

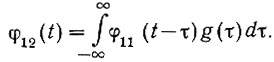(4.31б)

В предыдущем разделе было показано, что если на вход системы подана импульсная функция

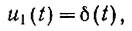
то уравнение (4.31а) сильно упрощается и напряжение на выходе системы становится равным импульсной переходной функции:

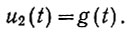
Поскольку уравнение (4.31а) имеет тот же вид, что и уравнение (4.31б), то можно сделать следующий вывод. Если на вход системы подать сигнал (белый шум), автокорреляционная функция которого является импульсной функцией

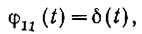
то взаимокорреляционная функция входа и выхода системы будет равна импульсной переходной функции:

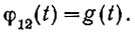
Благодаря этому становится возможным создать (рис. 4.8) схему, позволяющую определить импульсную переходную функцию системы.

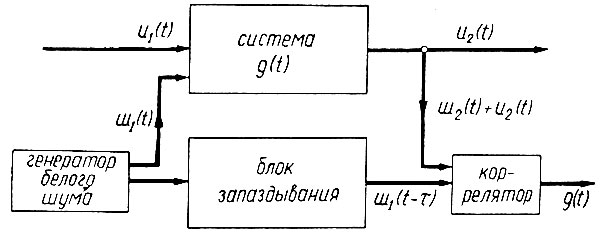
Рис. 4.8. Схема определения импульсной переходной функции системы

Рассмотрим работу схемы, показанной на рис. 4.8.

Подадим на вход системы от специального генератора белый шум ш₁(t), автокорреляционная функция которого равна импульсной функции. Одновременно при помощи блока запаздывания сдвинем функцию ш₁(t) на τ сек. После прохождения шума через систему на ее выходе появится напряжение ш₂(t). Поэтому, если на вход коррелятора подать функции ш₁(t - τ) и ш₂(t), то на его выходе появится напряжение, равное импульсной переходной функции системы [g(t)].

Если на вход системы кроме белого шума подать еще напряжение u₁(t), тогда на вход коррелятора попадет сумма напряжений

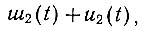
где u₂(t) - напряжение, которое появится на выходе системы после прохождения через нее сигнала u₁(t).

Но взаимокорреляционная функция от напряжений u₁(t) и u₂(t) равна нулю, ибо u₁(t) на вход коррелятора не подается и для него это напряжение равно нулю.

Следовательно, схема рис. 4.8 позволяет определить импульсную переходную функцию системы при любом виде внешнего сигнала на ее входе [u₁(t)]. Благодаря этому становится возможным определение g(t) даже на работающей системе без ее отключения.

Кроме того, посторонний шум, вносимый в систему или создаваемый ею, совершенно не влияет на точность измерения g(t), так как он не вносит ошибки.

При расчете системы на минимум среднеквадратичной ошибки (ур. 4.27) корреляционные функции характеризуют сигналы, подаваемые на вход системы, и ее поведение во временной области. Выполнив над корреляционными функциями двухстороннее преобразование Лапласа (ур. 4.7), можно получить аналогичные характеристики и в области комплексной частоты:

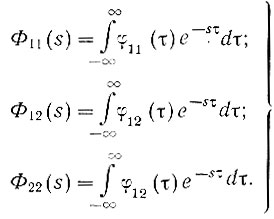(4.32)

Кроме того, что Φ₁₁(s) представляет собой изображение Лапласа автокорреляционной функции, эта функция сама по себе является очень важной частотной характеристикой. Рассмотрим эту особенность функции Φ₁₁(s).

Известно, что всякую непрерывную функцию u(t) в любом конечном интервале (Т) можно разложить в так называемый ряд Фурье, состоящий из отдельных гармоник (синусоид и косинусоид с разной амплитудой и частотой):

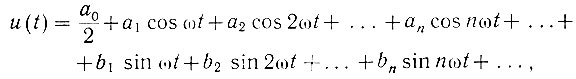(4.33)

где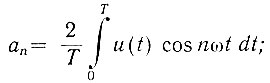

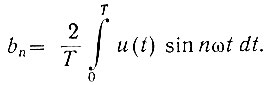
В комплексной форме ряд Фурье записывается в несколько ином виде:

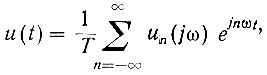(4.34)

где

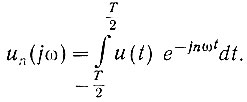(4.35)

Как следует из уравнения (4.34) функция u(t) представляется в виде бесконечного дискретного ряда гармоник, амплитуды которых определяются уравнением (4.35).

Пусть напряжение u(t) включено на какую-либо цепь с сопротивлением R. Поскольку это напряжение состоит из ряда гармоник, то можно считать, что каждая из этих гармоник выделяет на сопротивление R энергию, равную

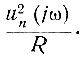
Так как спектр напряжения u(t) (ур. 4.34) является дискретным, то говорят, что энергия в сигнале u(t) сконцентрирована на отдельных частотах (в отдельных гармониках).

Как следует из уравнения (4.35), зависимость амплитуд гармоник от частоты (амплитудный спектр) имеет вид дискретной кривой (рис. 4.9), существующей только в точках, где n - любое целое число.

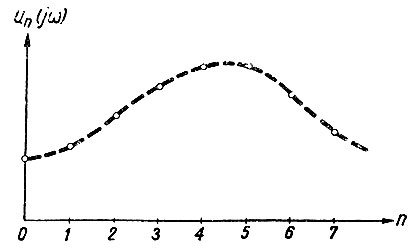
Рис. 4.9. Дискретный амплитудный спектр

До сих пор мы рассматривали разложение кривой u(t) в интервале времени Т. Если для периодической кривой в качестве этого интервала выбрать ее период, то вне этого интервала времени кривая будет повторяться. Поэтому она точно определяется ее дискретным спектром.

Что же касается апериодического напряжения, то в интервале Т секунд оно характеризовалось (с определенной ошибкой) дискретным спектром. Для того чтобы уменьшить эту ошибку, интервал Т необходимо увеличивать. В пределе, когда Т = ∞) ошибка исчезает, но ряд Фурье (ур. 4.34) превращается в интеграл Фурье:

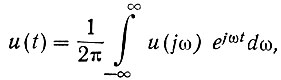(4.36)

где

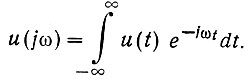(4.37)

Непрерывная функция u(jω) является пределом дискретной зависимости u_n(jω) (ур. 4.35 и рис. 4.9), расстояние между значениями которой стремится к нулю. Как следует из уравнения (4.37), в этом случае напряжение u(t) уже имеет непрерывный спектр гармоник, и энергия, содержащаяся в функции u(t), непрерывно распределяется по всему диапазону частот.

Если в дискретном спектре функция u_n(jω) определяла зависимость амплитуд гармоник от частоты, то в непрерывном спектре функция u(jω) уже дает зависимость плотности амплитуд гармоник (отношение величин амплитуд к бесконечно малому участку изменения частоты) от частоты (рис. 4.10). С подобным явлением мы уже сталкивались, рассматривая дифференциальную функцию распределения вероятности (см. выше). Там при переходе от дискретной функции напряжения к непрерывной вероятность заменялась плотностью вероятности, характеризующей отношение вероятности к бесконечно малому участку напряжения.

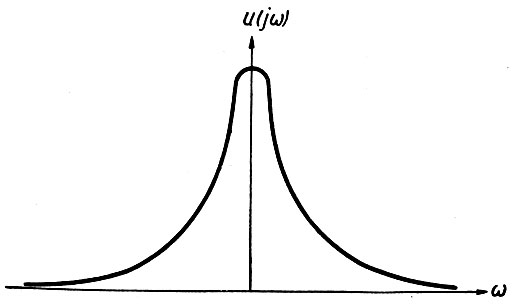
Рис. 4.10. Непрерывный спектр плотности амплитуды

Найдем далее непосредственную связь функции Φ₁₁(s) (ур. 4.32) с напряжением u₁(t), для которого определена автокорреляционная функция φ₁₁(τ).

Прежде всего запишем (ур. 4.24), что

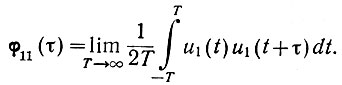
Подставив значение φ₁₁(τ) в уравнение (4.32), получим:

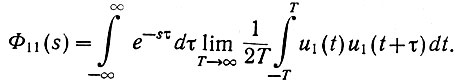
Изменяя порядок интегрирования, запишем:

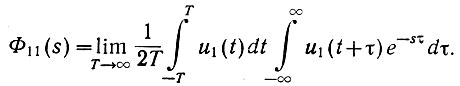
Основываясь на законе больших чисел, заменим бесконечные пределы второго интеграла конечными (Т является достаточно большой величиной). Тогда получим:

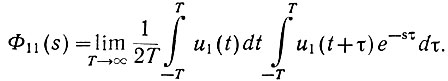
Введем вместо τ новую переменную времени: σ = t + τ. Тогда (dσ = dτ), принимая, что при T → ∞, ±T + t ≈ ±T, получим

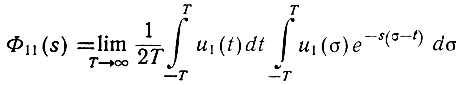
или

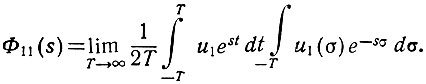
Здесь два интеграла являются сопряженными. Поэтому

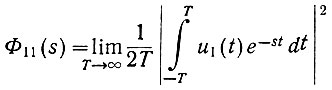(4.38)

или

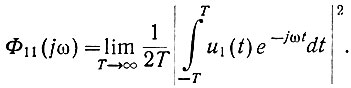(4.39)

Как следует из уравнения (4.37), правая часть уравнения (4.39) пропорциональна квадрату функции плотностей амплитуд гармоник. Поэтому Φ₁₁(jω) называют спектральной плотностью мощности. Легко увидеть, что Φ₁₁(jω) является действительной функцией квадрата частоты (ω²).

Таким образом, периодическое напряжение характеризуется дискретным амплитудным спектром, апериодическое - непрерывным спектром плотностей амплитуд, а случайное напряжение - спектральной плотностью мощности. Наряду с этим спектральная плотность может также характеризовать распределение мощности по частотному спектру и для периодических и апериодических напряжений.

Характеристика Φ₁₁(jω) показывает распределение плотности мощности по всему спектру гармоник. Поэтому мощность, рассеиваемая на сопротивлении R = 1 ом гармониками, имеющими частоту от ω₁ до ω₂, определяется интегралом.

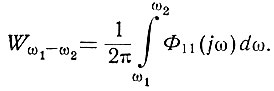(4.40)

Общая же мощность, содержащаяся во всем диапазоне частот [в сигнале u₁(t)], равна

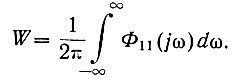(4.41)

Следует иметь в виду, что Φ₁₁(jω) является обобщающей характеристикой, определяющей спектральную плотность мощности сигнала u₁(t). Однако характеристики амплитудного спектра в ней отсутствуют.

По аналогии с Φ₁₁(jω) функция Φ₁₂(jω) (ур. 4.32) называется взаимной спектральной плотностью мощности.

Ранее было показано (ур. 4.10), что в области комплексной частоты напряжения на входе и выходе системы связаны зависимостью

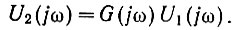
Аналогичная связь во временной области определялась интегралом свертки (ур. 4.22):

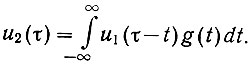
Корреляционные функции во временной области имеют ту же связь (ур. 4.28):

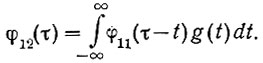
Поэтому лапласовы изображения корреляционных функций также связаны зависимостью

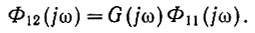(4.42)

Определим теперь соотношение между спектральными плотностями сигналов на входе [Φ₁₁(jω)] и выходе [Φ₂₂(jω)] системы.

Подставив в уравнение (4.32) значение автокорреляционной функции выходного сигнала (ур. 4.29), получим:

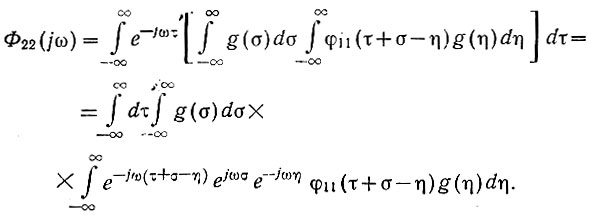
Меняя порядок интегрирования, получаем

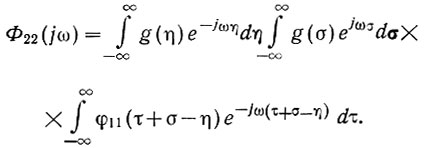
Заменив в уравнении (4.16) s на jω и рассматривая весь диапазон времени (∞ > t > -∞), можно записать:

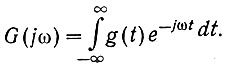
Поэтому предыдущее уравнение может быть записано в виде

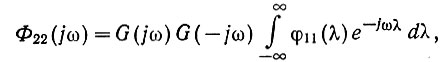
где λ = τ + σ - η,

dλ = dτ.

Поскольку последний интеграл представляет собой (ур. 4.32) спектральную плотность входной мощности сигнала, то уравнение, связывающее спектральные плотности входного и выходного сигналов, можно записать в следующем виде:

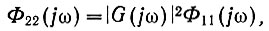(4.43)

где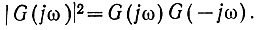

Спектральная плотность входного сигнала Φ₁₁(jω) может быть непосредственно определена из опыта. Поскольку Φ₁₁(jω) равна мощности сигнала u₁(t), заключенной между ω и ω + dω, то плотность будет определяться следующим образом.

Подадим (рис. 4.11) исследуемую случайную функцию u₁(t) на гармонический анализатор. Этот аппарат является узкополосным фильтром, пропускающим только небольшой спектр гармоник. Поскольку все же полоса пропускания не бесконечно мала, на выходе анализатора включается интегратор, осредняющий спектр гармоник.

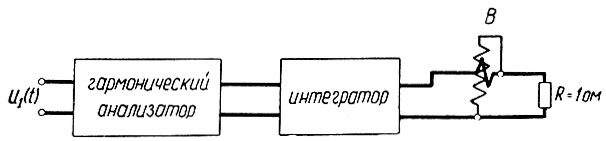
Рис. 4.11. Схема определения функции спектральной плотности мощности

Если выход интегратора включить на сопротивление R = 1 ом, то, измеряя при помощи ваттметра (В) мощность, рассеиваемую на сопротивлении полосой спектра, можно определить точку кривой Φ₁₁(jω).

Меняя настройку анализатора, определяем ряд точек, а по ним строим искомую кривую Φ₁₁(jω) = f(ω).

В случае, когда напряжение u₁(t) задано аналитически, спектральная плотность мощности может быть вычислена по уравнениям (4.32 или 4.39).

Рассмотрим простейший пример такого вычисления: необходимо определить спектральную плотность белого шума.

Как было показано ранее, автокорреляционная функция белого шума равна импульсной функции:

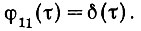
Поэтому, подставив значение φ₁₁(τ) в уравнение (4.32), получаем

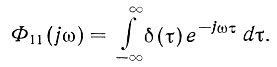(4.44)

Вычисляя этот интеграл, определяем, что

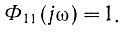
Некоторые виды спектральных плотностей для наиболее характерных функций показаны на рис. 4.12. Как видно из этого рисунка, спектральная плотность мощности белого шума представляет собой горизонтальную прямую линию с ординатой, равной единице. Спектральная плотность мощности постоянного напряжения выражается импульсной функцией, расположенной в начале координат. Две импульсные функции, расположенные в точках 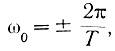характеризуют периодическое синусоидальное напряжение с частотой ω₀.

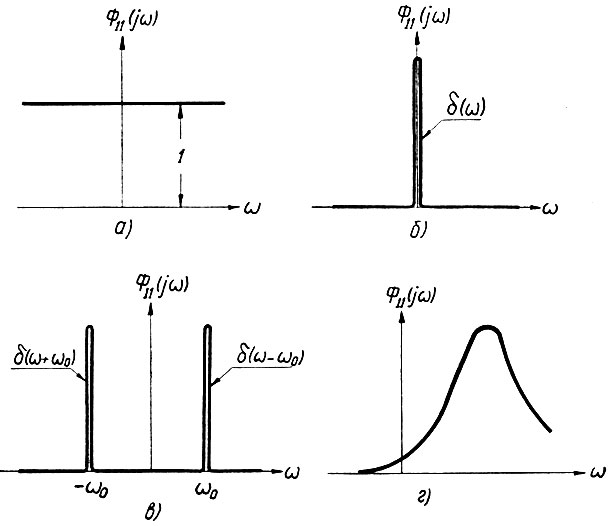
Рис. 4.12. Спектральная плотность мощности: а - белого шума; б - постоянного напряжения; в - периодического напряжения; г - случайного напряжения

Для случайного напряжения Φ₁₁(jω) представляет собой плавную кривую, показывающую распределение плотности мощности по спектру.