
3. Минимизация среднеквадратичной ошибки
Основной задачей синтеза систем автоматического управления является создание такой системы [определение таких функций G(s) или g(t)], в которой среднеквадратичная ошибка на выходе была бы минимальной.
Среднеквадратичная ошибка может быть определена по импульсной переходной и корреляционным функциям (ур. 4.27). Однако значительно проще эту ошибку определить по характеристикам системы в области комплексной частоты. При этом следует иметь в виду, что среднеквадратичная ошибка состоит из двух составляющих: ошибки, появляющейся при прохождении шума [ш1(t)] через систему, и ошибки, обусловленной прохождением полезного сигнала [u1(t)]. Поскольку здесь исследуются только линейные системы, то каждую составляющую ошибки можно подсчитать отдельно. Поэтому рассмотрим два случая работы системы, когда на ее вход подан либо шум, либо полезный сигнал.
а) Прохождение шума через систему
В этом случае (рис. 4.13) на вход системы подается только шум [ш1(t)]. Естественно, что сигнал на выходе системы [ш2(t)] не является полезным и поэтому равен ошибке.
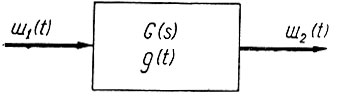
Рис. 4.13. Прохождение шума через систему
Полная мощность выходного сигнала, а следовательно, и среднеквадратичная ошибка равны (ур. 4.41)
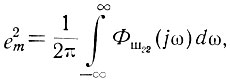
где Φш22 - спектральная плотность мощности шума на выходе системы.
Подставив в это выражение значение спектральной плотности мощности сигнала на выходе системы (ур. 4.43), получим
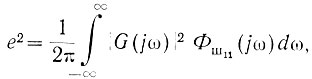 (4.45)
(4.45)где Φш11(jω) - спектральная плотность мощности шума на входе системы.
б) Ошибка прохождения полезного сигнала
Эта ошибка появляется вследствие того, что, во-первых, практически выполненная система может несколько иначе перерабатывать сигнал, нежели желательно, и, во-вторых, в целях минимизации среднеквадратичной ошибки система может отличаться от желаемой.
Рассматривая ошибку, появляющуюся после прохождения полезного сигнала через систему, целесообразно взять схему, представленную на рис. 4.14. Здесь ошибка получается как разность сигналов на выходе двух систем:
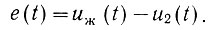 (4.46)
(4.46)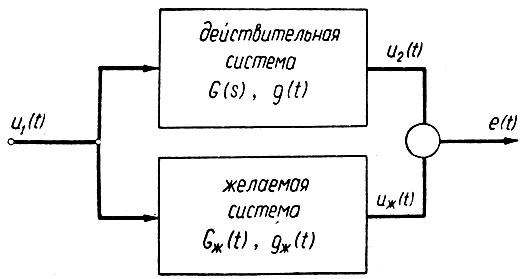
Рис. 4.14. Схема определения ошибки полезного сигнала
Одна из этих систем - физически существующая действительная система [G(s), g(t)], а другая - желаемая система [Gж(s), gж(t)].
В соответствии с уравнением (4.22) напряжение на выходе реальной системы определяется зависимостью
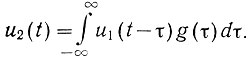
Аналогично этому, напряжение на выходе желаемой системы равно
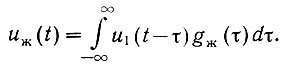
Подставив значения напряжений u2(t) и uж(t) в уравнение (4.46), получаем
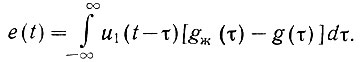
Таким образом (рис. 4.15), ошибку e(t) можно рассматривать как выходное напряжение условной системы [Gж(s) - G(s); gж(t) - g(t)], на вход которой подан полезный сигнал u1(t). Благодаря этому среднеквадратичная ошибка, получающаяся при прохождении полезного сигнала, может быть определена как полная мощность сигнала на выходе условной системы. Поэтому, аналогично уравнению (4.45), получаем
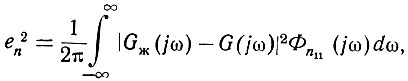 (4.47)
(4.47)где Gж(jω) - амплитудо-фазовая характеристика желаемой системы;
G(jω) - амплитудо-фазовая характеристика реальной системы;
Φ11(jω) - спектральная плотность мощности полезного сигнала на входе системы.
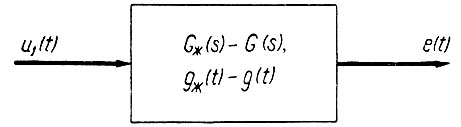
Рис. 4.15. Прохождение сигнала через условную систему
Общая ошибка, получающаяся на выходе системы, складывается из ошибок шума и полезного сигнала:
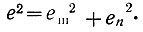
Поэтому, подставив значения этих ошибок (ур. 4.45 и 4.47), получаем
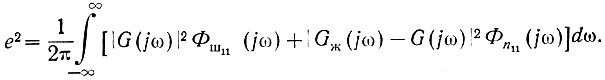 (4.48)
(4.48)Пример. Нужно вычислить среднеквадратичную ошибку на выходе схемы, показанной на рис. 4.16. На вход системы подан белый шум со спектральной плотностью Φш11(jω) = 2. Параметры схемы: R = 500 ом; С = 0,01 ф.
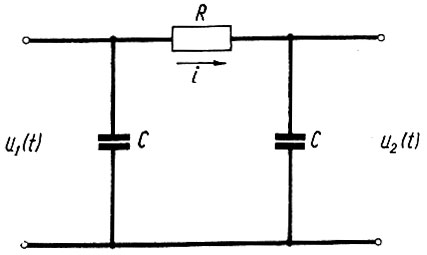
Рис. 4.16. Схема системы
Определим вначале передаточную функцию системы. Для схемы рис. 4.16 можно записать:
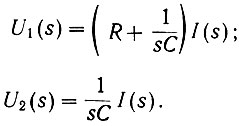
Решая эти уравнения совместно, определяем передаточную функцию
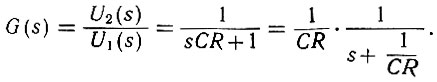
Подставив в это уравнение значения параметров схемы получаем
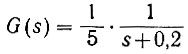
или
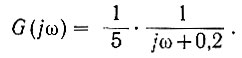
Тогда среднеквадратичная ошибка на выходе системы (ур. 4.45) равна
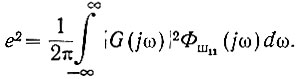
Подставив значения параметров, будем иметь
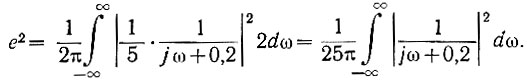
Учитывая (ур. 4.43), что
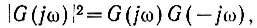
получаем
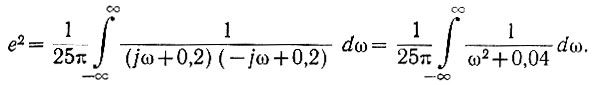
Вычисляя интеграл, получаем
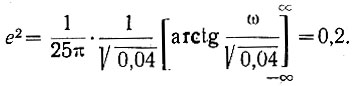
Для рассматриваемого примера определим также спектральную плотность сигнала на выходе системы.
Как следует из уравнения (4.43), спектральная плотность сигнала на выходе системы равна
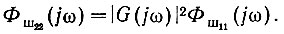
Подставив значения параметров, получаем
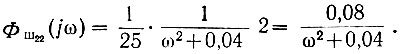
Оптимизация системы автоматического управления сводится к определению передаточной функции системы, среднеквадратичная ошибка на выходе которой была бы равна минимуму. При этом должны быть учтены ограничения, накладываемые условием физической реализуемости системы. Это условие заключается в том, что система должна находиться в покое (напряжение на ее выходе должно быть равно нулю) до момента подачи сигнала на ее вход. Математически условие физической реализуемости записывается в следующем виде:
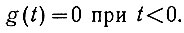
Опуская доказательство, отметим, что для системы, рассматриваемой в области комплексной частоты, условием физической реализуемости является аналитичность передаточной функции системы в правой полуплоскости комплексной частоты. В этом случае все полюсы* передаточной функции должны лежать в левой полуплоскости.
* (Полюсом функции комплексной частоты называется точка, в которой эта функция становится равной бесконечности. Так, например, для функции 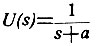 в точке s = -а функция равна бесконечности.)
в точке s = -а функция равна бесконечности.)
Рассмотрим вначале, как выполняется минимизация среднеквадратичной ошибки (получение ее минимума) без учета ограничений, накладываемых условием физической реализуемости системы.
Предположим, что нам задана амплитудо-фазовая характеристика системы (ур. 4.11):
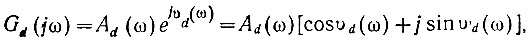 (4.49)
(4.49)где Ad(ω) и υd(ω) - модуль и фаза заданной амплитудо-фазовой характеристики (действительные функции частоты).
Однако, для того чтобы уменьшить до возможного минимума среднеквадратичную ошибку на выходе системы, мы изменим заданную амплитудо-фазовую характеристику и примем ее равной
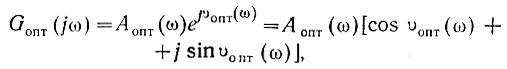 (4.50)
(4.50)где Аопт(ω) и υопт(ω) - модуль и фаза оптимальной амплитудо-фазовой характеристики (действительные функции частоты).
Тогда среднеквадратичная ошибка на выходе системы (ур. 4.48) будет равна
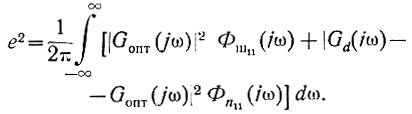 (4.51)
(4.51)Подставив в это уравнение значения амплитудо-фазовых характеристик (ур. 4.49 и 4.50), получим (для упрощения записи аргументы ω и jω опущены):
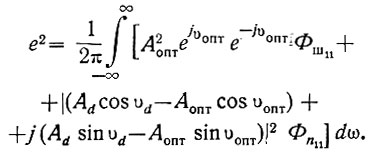 (4.52)
(4.52)Преобразуем следующее выражение:
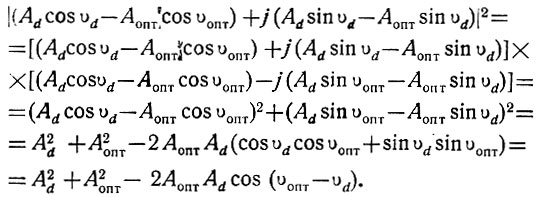
Поэтому, учитывая, что ejυопт еjυопт = 1, уравнение (4.52) может быть записано в следующем виде:
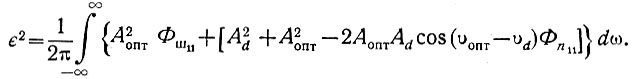
Коэффициенты Аопт, Ad, Фш11 и Фn11 положительны при любых значениях частоты (ω). Поэтому для минимизации среднеквадратичной ошибки необходимо, чтобы отрицательный член 2Аопт Ad cos(υопт - υd) был наибольшим, т. е. чтобы
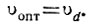 (4.53)
(4.53)Следовательно, для получения минимума среднеквадратичной ошибки не нужно изменять фазу амплитудо-фазовой характеристики системы. Эта фаза должна быть равна заданной (υd).
Учитывая, что при равенстве углов cos(υопт - υd) = 1, предыдущее уравнение можно записать в следующем виде:
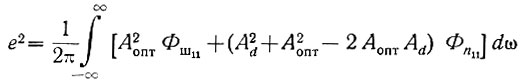
или
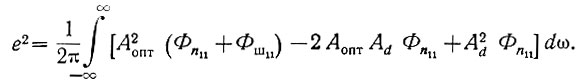
Поскольку все члены, входящие в подынтегральное выражение, положительны, то минимум среднеквадратичной ошибки определяется функцией
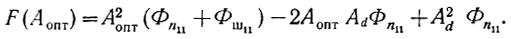
Следовательно, параметр Aопт определяется из равенства
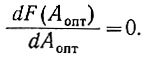
Определяя производную функции F(Aопт) и приравнивая ее нулю, получаем
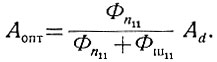 (4.54)
(4.54)Таким образом, выбирая параметры Aопт и υопт согласно уравнениям (4.53) и (4.54), определяем минимальное значение среднеквадратичной ошибки:
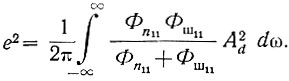 (4.55)
(4.55)Оптимальная амплитудо-фазовая характеристика системы определяется из соотношения (ур. 4.49 и 4.50)
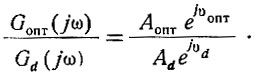
Подставив в это уравнение значения υопт (ур. 4.53) и Аопт (ур. 4.54), получаем
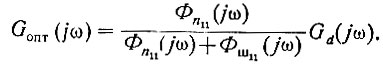 (4.56а)
(4.56а)Если в этом уравнении jω заменить на s, то получим выражение для оптимальной передаточной функции системы:
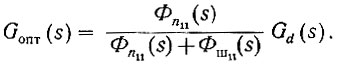 (4.56б)
(4.56б)Как следует из уравнений (4.56а) и (4.56б), при отсутствии шума на входе системы (Фш11 = 0) оптимальная передаточная функция (и амплитудо-фазовая характеристика) равна заданной. Следовательно, рассматриваемая оптимизация связана с уменьшением влияния шума на функцию выхода системы. При отсутствии шума оптимизация системы не нужна.
Таким образом, можно сказать, что уравнение (4.56б) определяет оптимальную передаточную функцию системы при наличии шума [Gопт(s)] по заданной передаточной функции при отсутствии шума [Gd(s)].
Рассмотрим пример определения оптимальной передаточной функции.
Пусть спектральные плотности полезного сигнала и шума на входе системы равны:
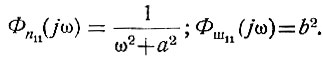
Кроме того, заданная передаточная функция системы равна
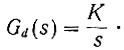
Заменив s на jω, получаем заданную амплитудо-фазовую характеристику системы
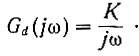
Подставив эти данные в уравнение (4.56а), определим оптимальную амплитудо-фазовую характеристику системы
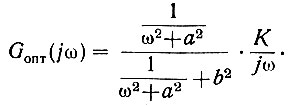
Заменив jω на s, а следовательно, и -ω2 на s2, получим оптимальную передаточную функцию системы
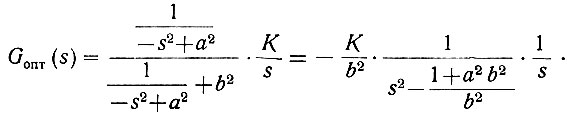
В полюсах функция Gопт(s) равна бесконечности. Поскольку же K ≠ 0 и b ≠ ∞, полюсы этой функции определяются из равенства
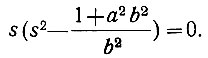
Таким образом, функция имеет три полюса:
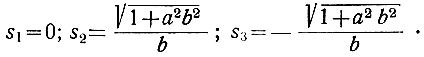
Поскольку один из полюсов (s2 > 0) находится в правой полуплоскости, то оптимальная передаточная функция Gопт(s) физически не реализуема.
Следует отметить, что член (ур. 4.56б)
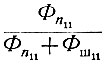 (4.57)
(4.57)всегда является функцией ω2. Поэтому оптимальная передаточная функция всегда имеет двойные полюсы (как s2 и s3 в предыдущем примере). Следовательно, наличие этого члена приводит к тому, что Gd(s) всегда физически не реализуема.
Единственный частный случай реализуемой оптимальной функции будет иметь место только тогда, когда шум на входе системы отсутствует, т. е. член (ур. 4.57) равен единице. В этом случае, если сама функция Gd(s) физически реализуема, то, естественно, реализуема и оптимальная система.
Во всех остальных случаях приходится выбирать физически реализуемую передаточную функцию системы, по возможности приближающуюся к оптимальной.
В общем виде методики приближения физически реализуемой передаточной функции системы к оптимальной не существует. Поэтому рассмотрим, как решается эта задача Боде и Шенноном на следующем примере.
Необходимо создать физически реализуемую систему экстраполяции (предсказывания) случайной функции, имеющей наименьшую среднеквадратичную ошибку. Считаем, что шум на входе системы отсутствует.
Поставленная задача математически записывается в следующем виде:
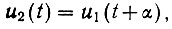 (4.58)
(4.58)где u2(t) - сигнал на выходе системы;
u1(t) - сигнал на входе системы;
α - время упреждения (предсказывания) сигнала.
Передаточная функция системы, осуществляющей преобразование вида (4.58), как следует из уравнений (4.9) и (4.7), равна
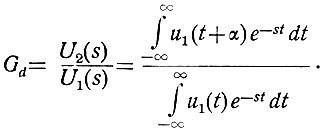
Проведем в верхнем интеграле замену переменной t на τ-α (при этом dt = dτ). Тогда получим передаточную функцию системы в следующем виде:
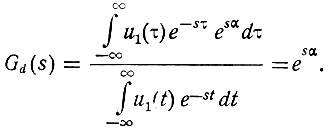
Поскольку по условию задачи шум на входе системы отсутствует, то (ур. 4.56б)
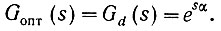 (4.59)
(4.59)Эта функция имеет полюс при s1 = ∞. Поскольку полюс находится в правой полуплоскости комплексной частоты, то функция (4.59) физически не реализуема. Поэтому необходимо найти такую физически реализуемую функцию G(s), которая по возможности приближалась бы к оптимальной Gопт(s).
Выполним эту задачу следующим образом. Прежде всего представим физически существующую систему, передаточную функцию которой мы ищем, в виде двух частей (рис. 4.17): G1(s) и G2(s).
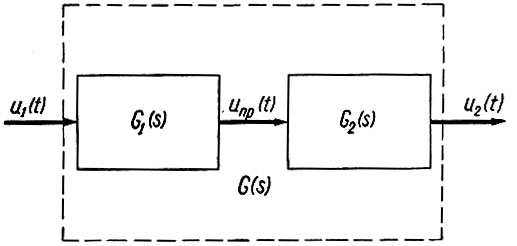
Рис. 4.17. Определение функции, приближенно отображающей Gопт(s)
Спектральная плотность полезного сигнала, поданного на вход системы, может быть представлена в виде двух составляющих
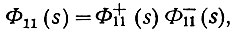 (4.60)
(4.60)где Ф+21(s) - комплексная составляющая спектральной плотности, полюсы которой расположены только в левой части полуплоскости комплексной частоты;
Ф-11(s) - комплексная составляющая, полюсы которой находятся только в правой полуплоскости.
Так, например, если или
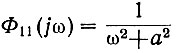
или
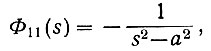
то
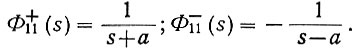
Выполняя это разложение, легко увидеть, что всегда должно соблюдаться равенство
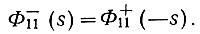 (4.60а)
(4.60а)Выберем передаточную функцию первой части системы равной
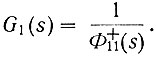 (4.61)
(4.61)Поскольку все полюсы Ф+11(s) расположены в левой части полуплоскости комплексной частоты, то G1(s) является физически реализуемой функцией.
Если теперь выбрать передаточную функцию второй части системы равной
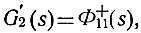 (4.62а)
(4.62а)то передаточная функция всей системы (ур. 4.61 и 4.62а) будет равна единице:
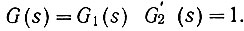
В этом случае получилось бы, что
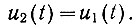
Однако по условию задачи (ур. 4.58) необходимо получить упреждение выходного сигнала на а секунд. Поэтому мы несколько изменим передаточную функцию второй части системы и выберем ее равной не
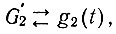 (4.62б)
(4.62б)где g2(t) - импульсная переходная функция второй части системы, равная обратному преобразованию Лапласа от G'2(s),
а
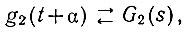 (4.63)
(4.63)где G2(s) - лапласово изображение функции g2(t + α).
Для того, чтобы эта функция была физически реализуема, введем ограничение:
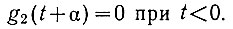
Интересно отметить, что в рассматриваемой системе (рис. 4.17) промежуточный сигнал является белым шумом.
Действительно, спектральная плотность мощности промежуточного сигнала uпр(t) равна (ур. 4.43)
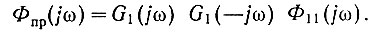
Поскольку (ур. 4.61)
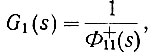
то
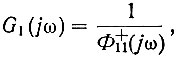
а (ур. 4.60а)
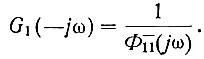
Вместе с тем (ур. 4.60)
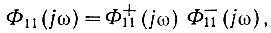
поэтому
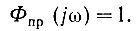
Следовательно, выбрав передаточную функцию первой части системы согласно уравнению (4.61), мы превратили сигнал u1(t) в белый шум [Uпр(t)].
Белый шум приближенно можно рассматривать как последовательность близко расположенных узких случайных импульсов. Каждый из этих импульсов дает на выходе системы напряжение
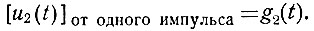
Сумма реакций от всех импульсов белого шума дает напряжение u2(t).
Среднеквадратичное же значение функции на выходе системы определяется условием
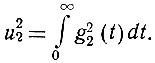 (4.64)
(4.64)Напряжение u2(t) должно опережать uпр(t) на α секунд. Следовательно, в момент t = 0 напряжение на входе второй части системы равно uпр(0), а напряжение на выходе системы должно равняться u2(-α). Однако для того чтобы выполнить условие физической реализуемости, напряжение на выходе системы [u2(t)] на отрезке времени от -α до 0 должно отсутствовать. Поэтому среднеквадратичная ошибка на выходе системы сводится к пренебрежению импульсами белого шума в пределах от 0 до α секунд:
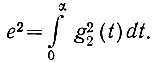 (4.65)
(4.65)Поэтому относительная среднеквадратичная ошибка на выходе равна
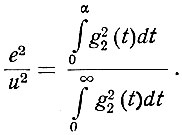 (4.66)
(4.66)Рассмотрим пример определения физически осуществимой передаточной функции системы.
Дано преобразование Лапласа автокорреляционной функции входного сигнала
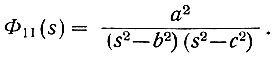
Необходимо построить систему с упреждением сигнала на α секунд.
Задачу решаем следующим образом.
а) Делим (ур. 4.60) Ф11(s) на два сомножителя:
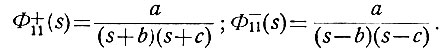
б) Определяем (по таблицам) исходную функцию, лапласово изображение которой (ур. 4.62а и 4.62б) равно Ф11+(s):
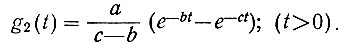 (4.67)
(4.67)в) Подсчитываем (ур. 4.61) передаточную функцию первой части системы
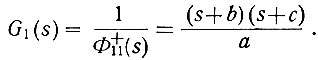 (4.68)
(4.68)г) Определяем (ур. 4.67) импульсную переходную функцию второй части системы без учета физической реализуемости:
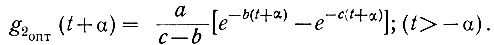 (4.69)
(4.69)д) Условие физической реализуемости требует, чтобы g2опт(t + α) = 0 при t < 0. Поэтому с учетом реализуемости импульсная переходная функция (ур. 4.69) должна быть равна
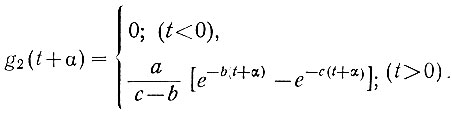 (4.70)
(4.70)Полученные переходные функции показаны на рис. 4.18. Как следует из этих кривых, функция g2(t) (верхний рисунок) физически реализуема (ур. 4.67). Однако сдвиг этой функции на а (нижний левый рисунок) уже делает ее нереализуемой (ур. 4.69). Если же "отрезать" от функции g2опт(t + α) ее часть, относящуюся к t < 0 (нижний правый рисунок), то она становится физически реализуемой (ур. 4.70).
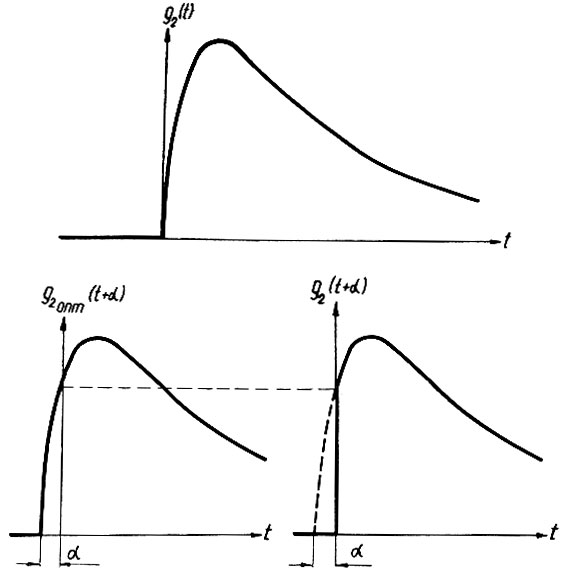
Рис. 4.18. Переходные функции второй части системы
е) Находим теперь (ур. 4.63) передаточную функцию второй части системы - лапласово изображение функции g2опт(t + α). Для этого запишем уравнение (4.70) в несколько ином виде:
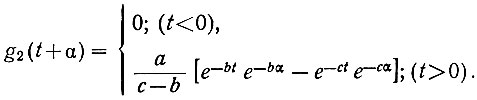
Тогда, пользуясь таблицами преобразованных функций, получаем
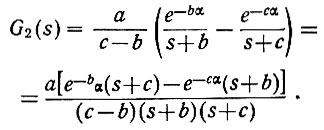 (4.71)
(4.71)ж) Определяем далее общую передаточную функцию системы
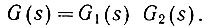
Подставив значения G1(s) (ур. 4.68) и G2(s) (ур. 4.71), получаем
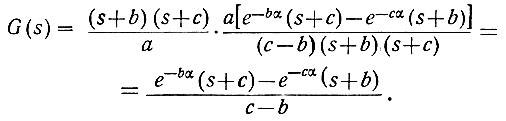
з) Среднеквадратичная ошибка упреждения (ур. 4.65 и 4.67) равна
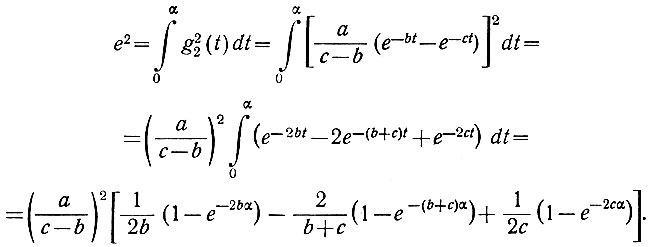
и) Среднеквадратичное значение функции на выходе системы определяется уравнением (4.64). Поэтому, подставив в предыдущее выражение ∞ вместо α, получаем
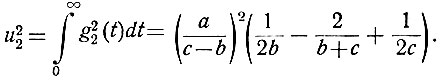
к) Наконец, относительная ошибка (ур. 4.66) равна
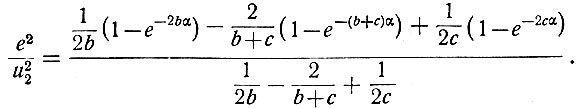

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
