2. Метод описывающей функции

Метод описывающей функции основывается на том, что нелинейный элемент системы автоматического управления заменяется линейным, приближенно описывающим его характеристики.

Рассматриваемый метод предполагает следующие допущения.

1. В системе имеется только один нелинейный элемент (если в системе имеется несколько нелинейных элементов, то их необходимо объединить и рассматривать как один элемент).

2. Характеристики нелинейного элемента не изменяются во времени. Следовательно, этот метод не применим к нелинейностям, связанным с нагревом элементов, дрейфом характеристик и т. д.

3. Если на вход нелинейного элемента включить синусоидальное напряжение, то на его выходе будет также синусоидальный сигнал. Иначе говоря, на выходе учитывается только основная гармоника сигнала. Это допущение обычно является правильным потому, что в большинстве случаев высшие гармоники выходного сигнала имеют малую (по сравнению с основной гармоникой) амплитуду и ими можно пренебречь.

Следовательно, описывающая функция, определяющая характеристики нелинейного элемента (рис. 5.4), может быть представлена в следующем виде:

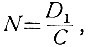(5.1)

где N - описывающая функция;

С - амплитуда напряжения на входе нелинейного элемента;

D₁ - амплитуда основной гармоники напряжения на выходе элемента.

Рис. 5.4. Схема замещения нелинейного элемента

Как следует из этого уравнения, величина описывающей функции зависит от амплитуды напряжения, поданного на вход нелинейного элемента. В случае, когда нелинейный элемент содержит источник э. д. с., описывающая функция, кроме того, становится зависимой от частоты (ω).

Таким образом, введение описывающей функции позволяет заменить нелинейный элемент линейным с определенными коэффициентом усиления и сдвигом фазы.

Рассмотрим пример определения описывающей функции.

Пусть задана (рис. 5.5) замкнутая система автоматического управления с нелинейным элементом, не имеющим источников э. д. с., и тремя линейными элементами, передаточные функции которых равны G₁(s), G₂(s) и G_ос(s). На вход элемента подается синусоидальное напряжение u₁(t) с частотой ω.

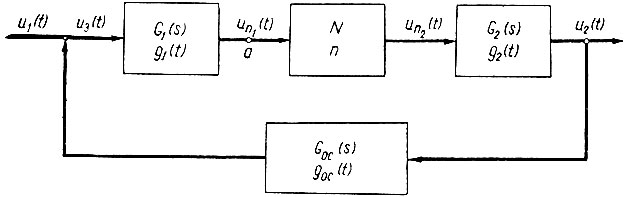
Рис. 5.5. Схема системы с нелинейным элементом

Кроме того, предположим, что нелинейный элемент имеет характеристику с насыщением (рис. 5.6). Поэтому в зависимости от величины амплитуды напряжения на входе нелинейного элемента [u_n1(t)] последний может работать в двух режимах.

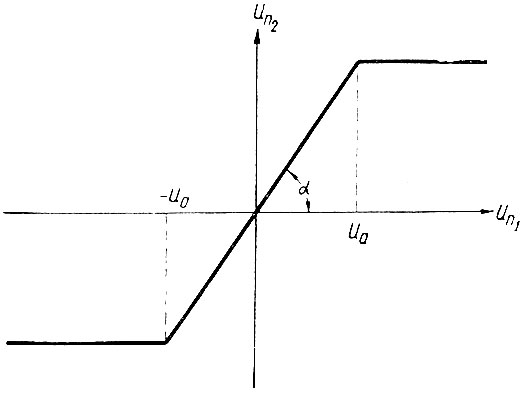
Рис. 5.6. Характеристика нелинейного элемента

В том случае, когда амплитуда напряжения u_n1(t) не превышает u_а, нелинейный элемент превращается в линейный усилитель с коэффициентом усиления

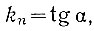
где α - угол наклона линейной части характеристики нелинейного элемента.

Если же напряжение u_n1(t) хотя бы в части периода превышает u_а, то нелинейный элемент работает следующим образом. В течение первой части периода (β ≥ ωt ≥ 0; рис. 5.7), пока напряжение u_n1(t) не достигло значения u_а, характеристика элемента является линейной. Для этой части периода можно записать:

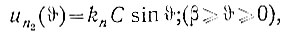(5.2)

где k_n = tg α - коэффициент усиления линейной части характеристики элемента;

С - амплитуда напряжения на входе нелинейного элемента;

υ = ωt.

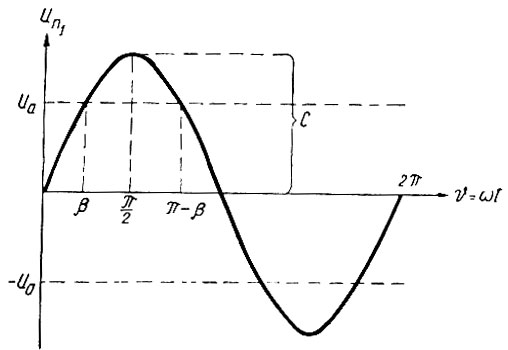
Рис. 5.7. Режимы работы нелинейного элемента

После того, как напряжение u_n1(t) становится больше u_а, рабочая точка характеристики нелинейного элемента (рис. 5.6) переходит на нелинейную насыщенную часть. В этом случае напряжение на выходе нелинейного элемента остается постоянным и равным

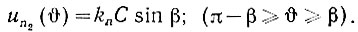(5.3)

Таким образом (ур. 5.2 и 5.3), для первой четверти периода можно записать:

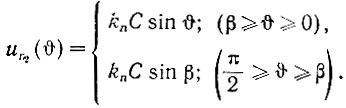(5.4)

Это напряжение является несинусоидальным. Поэтому для определения описывающей функции нелинейного элемента найдем амплитуду первой гармоники данного напряжения. Как следует из уравнения (4.33), эта амплитуда (Т = 2π) равна

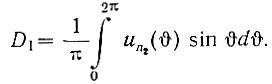
Меняя пределы интеграла (интегрируя от нуля до ^T/₄), получаем

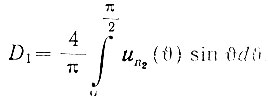
Подставим в это выражение значение u_n2(υ) (ур. 5.4):

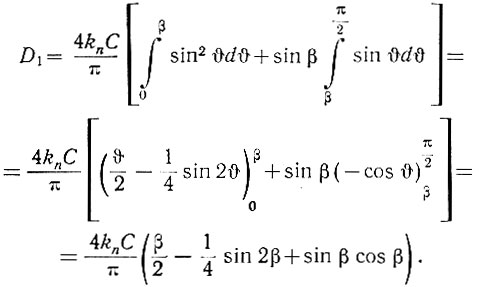
Поскольку

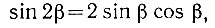
то

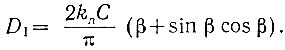(5.5)

Таким образом, амплитуда первой гармоники напряжения на выходе нелинейного элемента зависит от уровня сигнала на входе этого элемента (С) и величины напряжения насыщения (u_а).

После того как подсчитана амплитуда первой гармоники на выходе нелинейного элемента (D₁), легко определить (ур. 5.1) описывающую функцию:

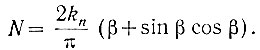(5.6)

Эта функция при k_n = 1 показана на рис. 5.8.

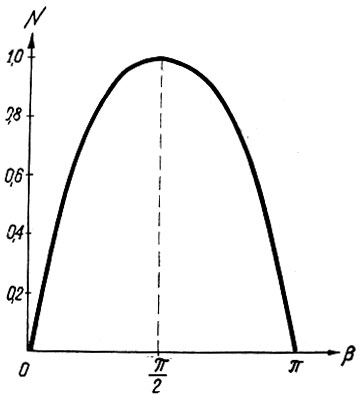
Рис. 5.8. Описывающая функция

Величина β, определяющая при заданной частоте (ω) момент времени (рис. 5.7), когда напряжение u_n1 = С sin υ достигает значения u_а, подсчитывается исходя из условия

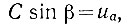
откуда

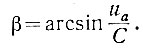(5.7)

Оценим ошибку, вносимую тем, что из спектра гармоник на выходе берется только первая гармоника.

Так как u_n2(υ) (ур. 5.4) является кривой, симметричной относительно оси абсцисс, то она не содержит нулевой (постоянной) составляющей и четных гармоник. Кроме того, поскольку эта кривая симметрична относительно вертикальной оси, проходящей через точку 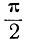, в ней также отсутствуют косинусоидальные составляющие. Поэтому (ур. 4.33) можно записать, что

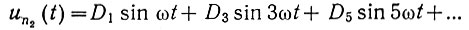
или, учитывая, что ωt = υ, получаем

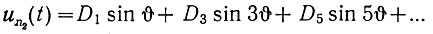
Для оценки ошибки, вносимой отбрасыванием третьей, пятой и т. д. гармоник, определим амплитуду третьей (наибольшей после первой) гармоники. Из уравнения (4.33) имеем (интегрирование ведется в пределах четверти периода)

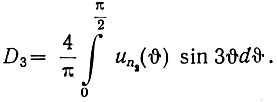
После подстановки в это уравнение значения u_n2(υ) (ур. 5.4) и интегрирования получаем

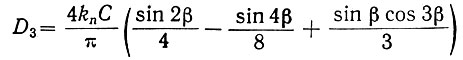
или после несложных преобразований будем иметь

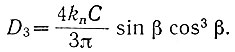
Подсчитаем отношение амплитуд третьей и первой гармоник:

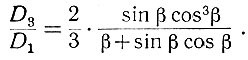
Это отношение косвенно характеризует точность исследования, выполняемого при помощи описывающей функции. Если в данное уравнение подставить значение β (ур. 5.7), то получим зависимость, показанную на рис. 5.9.

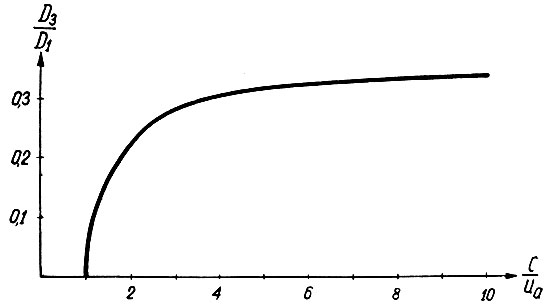
Рис. 5.9. Отношение амплитуд третьей и первой гармоник

Рассмотрим, как описывающая функция может быть использована для анализа устойчивости нелинейной системы автоматического управления. Анализ проведем на примере системы, показанной на рис. 5.5.

Разомкнем эту систему в точке a. Тогда получим разомкнутую систему с передаточной функцией

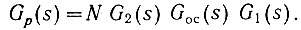(5.8)

Анализ устойчивости проведем при помощи критерия Найквиста по амплитудо-фазовой характеристике разомкнутой системы. Как известно, согласно этому критерию замкнутая линейная система автоматического управления будет устойчивой в том случае, когда амплитудо-фазовая характеристика разомкнутой системы [G_p(jω)] не охватывает точку -1; +j0. Поскольку введение в расчет описывающей функции (N) равносильно замене нелинейного элемента линейным, то критерий Найквиста может быть применен и к рассматриваемой системе (рис. 5.5) с нелинейным элементом (рис. 5.6).

Исследование устойчивости выполняется следующим образом. Как было показано выше, граница устойчивости системы определяется равенством (амплитудо-фазовая характеристика проходит через точку -1; +j0)

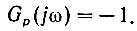(5.9)

В соответствии с уравнением (5.8) условие (5.9) можно записать в следующем виде:

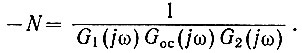(5.10)

Далее построим (рис. 5.10) на комплексной плоскости (+; +j) две кривые: функцию (ур. 5.6)

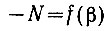
и зависимость

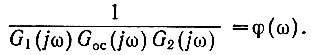
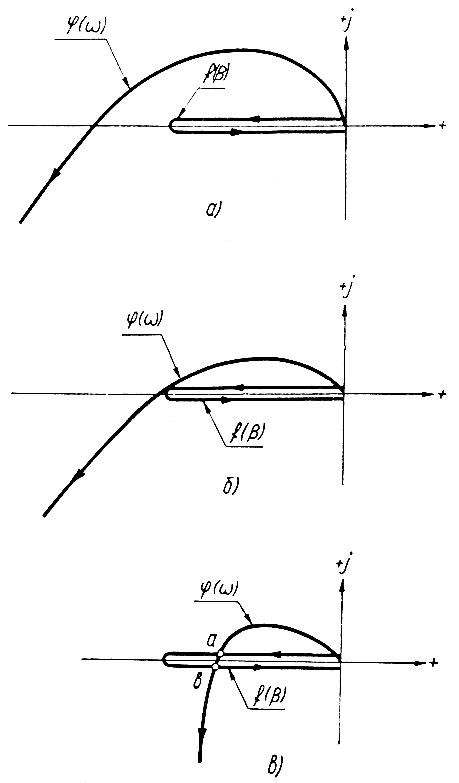
Рис. 5.10. Определение устойчивости системы

При этом по оси абсцисс комплексной плоскости откладываются f(β) и действительная составляющая функции φ(ω), а по оси ординат - мнимая составляющая φ(ω).

Как следует из уравнения (5.10), граница устойчивости будет определяться точками пересечения этих кривых. Поэтому здесь возможны три случая.

В первом случае (рис. 5.10, а) f(β) и φ(ω) не имеют точки пересечения. Поэтому система устойчива при любом значении β, а следовательно, и при любой величине сигнала на входе [u_n1(t)] нелинейного элемента.

Второй случай (рис. 5.10, б) соответствует системе, находящейся при максимальном значении β на границе устойчивости.

В третьем случае (рис. 5.10, в) система при

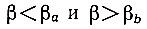
устойчива, а в диапазоне

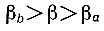
- неустойчива. Граничные значения β_а и β_b определяются точками пересечения кривых f(β) и φ(ω).

Ранее была показана методика расчета описывающей функции для разомкнутой системы. Рассмотрим теперь, как подсчитывается описывающая функция для замкнутой системы автоматического управления.

Сложность исследования замкнутой системы автоматического управления (рис. 5.5) заключается в том, что описывающая функция (N) зависит (ур. 5.6 и 5.7) от величины амплитуды (С) напряжения [u_n1(t)], поданного на вход нелинейного элемента. Однако из-за наличия обратной связи эта амплитуда, в свою очередь, зависит от величины передаточных функций элементов системы, и в частности от N. Кроме того, в ряде случаев, из-за наличия нелинейного элемента передаточная функция замкнутой системы при данной частоте (ω) напряжения, поданного на вход системы, может оказаться многозначной.

В настоящее время способ определения описывающей функции нелинейного элемента, работающего в замкнутой системе, разработан только для случая, когда на вход системы подается синусоидальное напряжение с неизменными амплитудой (Е) и частотой (ω):

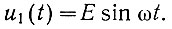
Рассмотрим методику определения описывающей функции на приведенном выше примере: замкнутая система (рис. 5.5) содержит нелинейный элемент с характеристикой насыщения (рис. 5.6).

Пусть при этом передаточные функции линейных элементов системы равны:

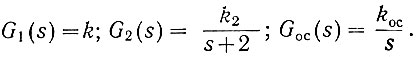
Как следует из рис. 5.5, соотношение между лапласовыми изображениями напряжений на выходе системы и входе элемента G₁(s) равно

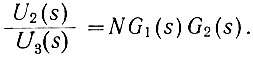(5.11)

Кроме того, имеет место следующее равенство:

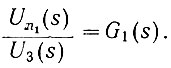(5.12)

Соотношение между лапласовыми изображениями напряжений на выходе и входе замкнутой системы определяется уравнением (4.14)

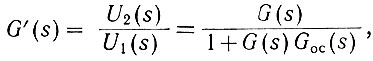
где 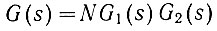- передаточная функция разомкнутой системы (при отсутствии обратной связи).

Подставив в это выражение значение G(s), получим

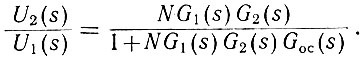(5.13)

Решая совместно уравнения (5.11), (5.12) и (5.13), определяем необходимое нам для дальнейших расчетов соотношение

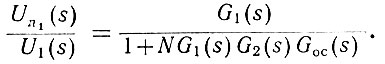(5.14)

Подставив в уравнение заданные в рассматриваемом примере значения G₁(s), G₂(s) и G_ос(s), получаем

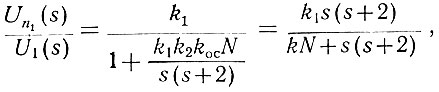
где k = k₁k₂k_ос.

Заменяя в этом уравнении s на jω, определяем следующую зависимость:

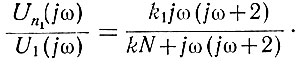
Преобразуем данное уравнение и представим его в несколько ином виде:

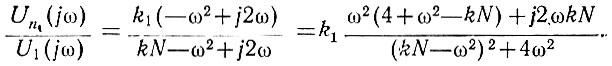
Это выражение в соответствии с уравнением (4.11) может быть записано в следующей форме:

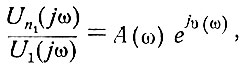
где

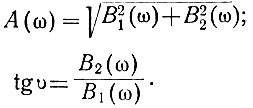
В рассматриваемом случае действительная составляющая равна

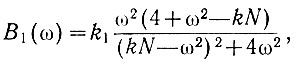
а мнимая определяется выражением

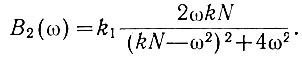
Поэтому отношение амплитуд напряжений u_n1(t) и u₁(t) равно

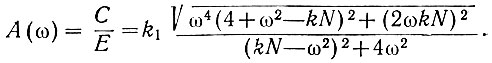
Преобразуя подкоренное выражение, получаем

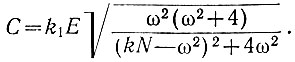(5.15)

В этом уравнении k, k₁, E и ω - заданы, а С и N - неизвестны.

Вместе с тем, описывающая функция (N) связана (ур. 5.6 и 5.7) с амплитудой (С) напряжения на входе нелинейного элемента следующей зависимостью:

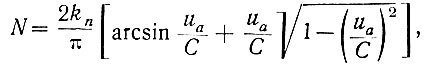(5.16)

где k_n = tgα и u_a - заданные параметры нелинейного элемента (рис. 5.6).

Если теперь решить совместно уравнения (5.15) и (5.16), то можно определить искомые значения описывающей функции (N).