3. Метод фазовой плоскости

Исследование систем автоматического управления при помощи метода описывающих функций по существу сводится к замене нелинейной системы эквивалентной линейной. В противоположность этому метод фазовой плоскости является способом исследования нелинейных систем.

Сущность метода фазовой плоскости заключается в следующем. Пусть система автоматического управления описывается нелинейным дифференциальным уравнением второго порядка. Ее состояние может быть задано двумя параметрами в двухмерном пространстве, т. е. на плоскости, называемой фазовой. Исследования, проводимые на этой плоскости, являются сущностью метода фазовой плоскости и позволяют получить необходимые характеристики системы.

Таким образом, метод фазовой плоскости применим только для систем, которые описываются уравнениями не выше второго порядка. Кроме того, должны быть заданы начальные условия параметров, изображаемых на этой плоскости.

Прежде чем приступить к изучению нелинейных систем, рассмотрим линейную систему, описываемую дифференциальным уравнением второго порядка:

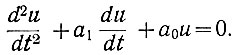(5.17)

Пусть для рассматриваемой системы заданы следующие условия, характеризующие ее в начальный момент времени:

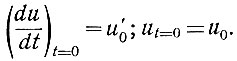
Рассмотрим вначале частный случай уравнения (5.17), когда коэффициент а₁ равен нулю. Для этого случая, переходя от переменной t в область комплексной частоты (s), можно записать

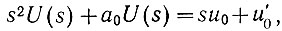
откуда можно определить лапласово изображение напряжения

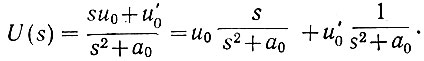
Определяя по таблице преобразованных функций исходную функцию, получаем

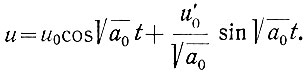
Введем обозначения:

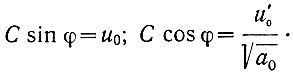(5.18)

Тогда получим

(5.19)

где (ур. 5.18)

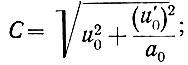(5.19а)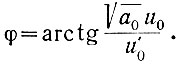

Из уравнения (5.19) следует, что

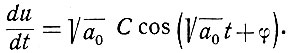(5.20)

Запишем уравнение (5.19) в следующем виде:

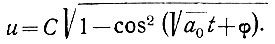
Подставив в это выражение значение 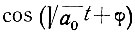(ур. 5.20), получаем

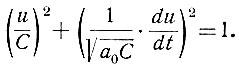(5.21)

Если теперь на плоскости (рис. 5.11) по оси абсцисс отлова жить переменную u, а по оси ординат - 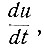то уравнение (5.21) станет эллипсом с полуосями

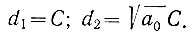
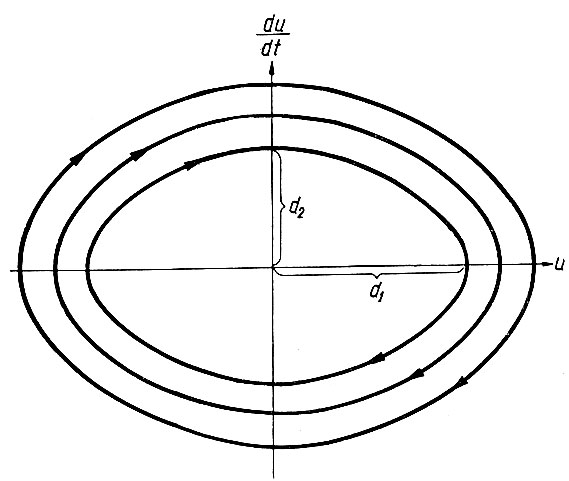
Рис. 5.11. Фазовый портрет системы с незатухающими колебаниями

В соответствии с изменением начальных условии (u₀ и u₀') коэффициент С (ур. 5.19а) изменяется и на плоскости рис. 5.11 получается семейство эллипсов. Это семейство называется фазовым портретом системы автоматического управления, описываемой уравнением (5.17) при a₁ = 0.

Таким образом, фазовый портрет определяет зависимость первой производной напряжения от величины этого напряжения. Как следует из рис. 5.11, время в явном виде в фазовом портрете отсутствует. Здесь только стрелками указывается направление движения рабочей точки системы во времени (направление фазовой траектории).

Точки на фазовой плоскости, в которых

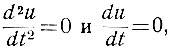(5.22)

называются особыми. Поскольку в этих точках производные напряжения (u) и скорости изменения напряжения 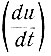равны нулю, особые точки соответствуют состоянию покоя системы. Следовательно, если система устойчива, то ее фазовая траектория приближается к особой точке.

Для рассматриваемого случая (ур. 5.19) особая точка определяется следующим образом. Прежде всего из условий (5.22) следует, что

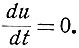
Следовательно, особая точка располагается на оси абсцисс.

Вторая производная напряжения (ур. 5.19) равна

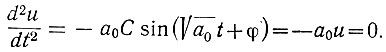
Поэтому (а₀ ≠ 0) вторая координата особой точки фазовой плоскости равна

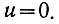
Следовательно, для рассматриваемого случая особой точкой является начало координат. В этом примере (рис. 5.11) рабочая точка системы, двигаясь по фазовой траектории, совершает колебания относительно начала координат. Поэтому эллипс соответствует незатухающим колебаниям системы. Амплитуда этих колебаний определяется начальными условиями (u₀ и u'₀).

В случае, когда коэффициент ах в уравнении (5.17) не равен нулю, эллипс превращается в спираль. При этом, если система устойчива, то ее рабочая точка (рис. 5.12, а) движется по спирали к особой точке (здесь - к началу координат). Если же система неустойчива, то рабочая точка (рис. 5.12, б) движется от особой точки по раскручивающейся спирали. Построив спирали для различных начальных условий, получим фазовый портрет системы. Для устойчивой системы, имеющей особую точку в начале координат, фазовый портрет показан на рис. 5.13.

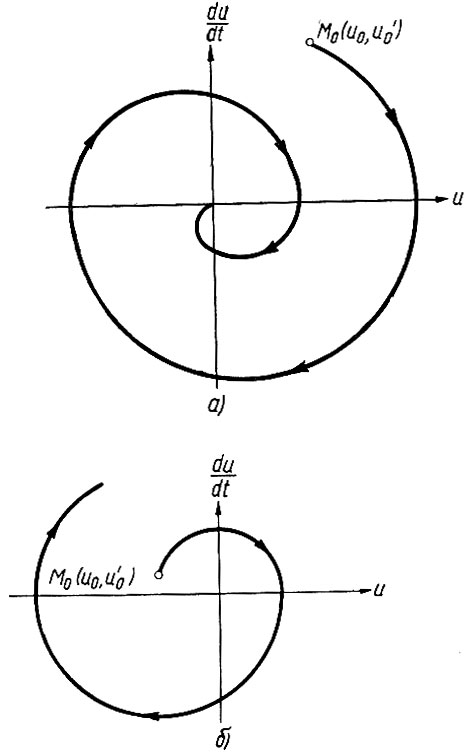
Рис. 5.12. Фазовые траектории устойчивой (а) и неустойчивой (б) систем

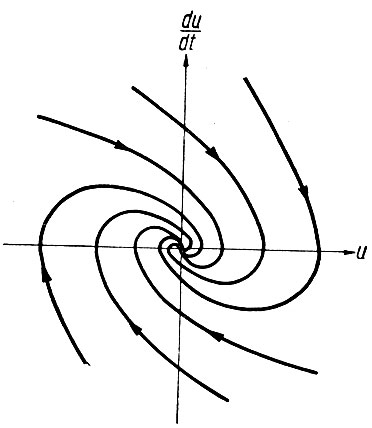
Рис. 5.13. Фазовый портрет устойчивой линейной системы

Выше уже указывалось на то, что время в явном виде на фазовом портрете отсутствует. Однако по фазовому портрету системы все же можно определить время движения рабочей точки по фазовой траектории из одного положения в другое.

Расчет времени движения рабочей точки из одного положения (А) в другое (В) производится следующим образом:

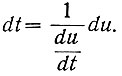
Поэтому, интегрируя обе части этого уравнения, получаем

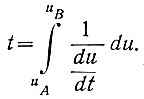
Следовательно, если построить (рис. 5.14) кривую 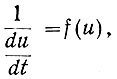то площадь, ограниченная этой кривой и осью абсцисс, определит искомое время.

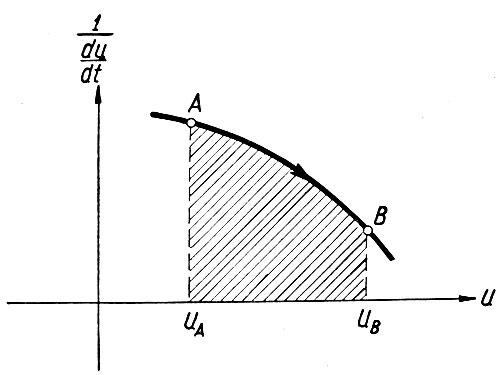
Рис. 5.14. Расчет времени движения рабочей точки

Исследование нелинейных систем автоматического управления на фазовой плоскости производится точно так же, как и линейных систем. Естественно, что при этом не производится аналитическое решение нелинейных уравнений в общем виде, ибо в большинстве случаев это просто невозможно.

Для того чтобы получить фазовый портрет нелинейной системы, можно воспользоваться схемой, показанной на рис. 5.15. В этой схеме на горизонтальную отклоняющую систему осциллографа подается напряжение исследуемой системы (u). Одновременно через дифференциальный блок на вертикальную систему подается скорость изменения этого напряжения ^du/_dt. Поэтому луч осциллографа вычерчивает фазовую траекторию системы. Меняя в системе начальные условия, можно провести полное исследование системы и получить ее фазовый портрет.

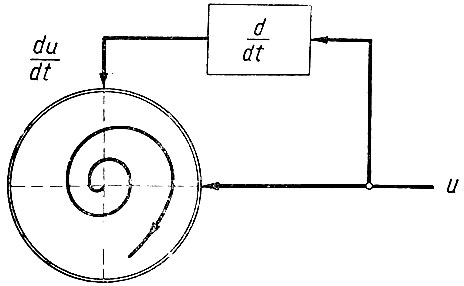
Рис. 5.15. Схема определения фазового портрета нелинейной системы

Следует иметь в виду одну важную особенность фазового портрета нелинейной системы. Если для линейной системы имелись либо устойчивые, либо неустойчивые фазовые траектории, то при исследовании нелинейных систем возможно получение различных фазовых траекторий, одни из которых являются устойчивыми, а другие - нет.

В качестве примера на рис. 5.16. показаны фазовые траектории одной из нелинейных систем. Как видно из этого рисунка одна траектория системы устойчива, а другая - нет. Между ними находится траектория, которая соответствует колебательному режиму с незатухающей амплитудой. Эта траектория называется предельным циклом.

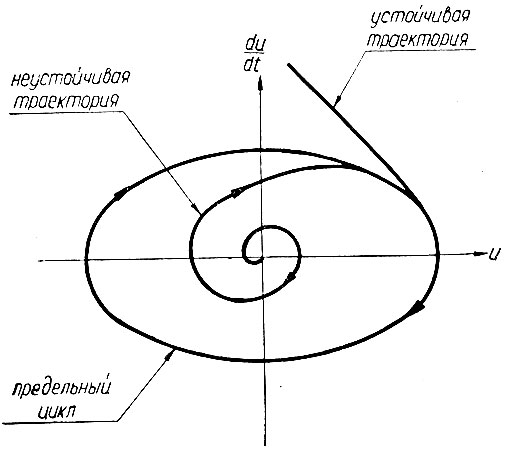
Рис. 5.16. Фазовая траектория нелинейной системы