9. Основные параметры, характеризующие экстремальное управление

Для удобства проведения математического описания экстремальной характеристики сдвинем ее так, чтобы экстремальная точка оказалась в начале координат (рис. 6.23). Показанная на этом рисунке характеристика имеет максимум. Однако все изложенное ниже в равной мере относится и к другому случаю, когда экстремальная характеристика имеет минимум.

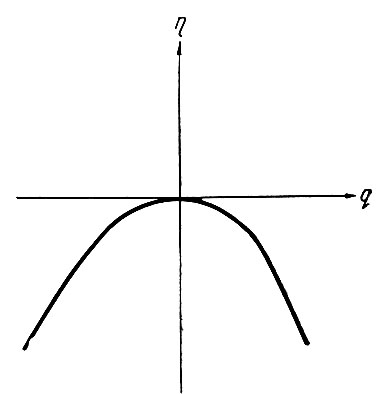
Рис. 6.23. Экстремальная характеристика

Хотя наши рассуждения относятся к любым экстремальным системам, по-прежнему будем обозначать буквой "η" экстремальный параметр, а буквой "q" - входной параметр, функцией которого является η.

Предположим, как и ранее, что входной параметр (q) изменяется с постоянной скоростью. Кроме того, примем, что в окрестности экстремальной точки экстремальная характеристика имеет форму параболы и описывается зависимостью

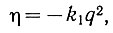(6.3)

где k₁ - коэффициент пропорциональности.

Пусть, далее, процесс управления начинается в момент, когда q равно нулю^*.

^* (Следует иметь в виду, что поскольку экстремальная точка (рис. 6.23) перенесена в начало координат, то q может иметь не только положительные, но и отрицательные значения.)

Вначале (рис. 6.24) q возрастает, но в точке А происходит реверс системы и q начинает уменьшаться. В точке В вновь осуществляется реверс, после чего q опять возрастает. Таким образом, q осуществляет периодические колебания (рыскания) возле нулевого значения (экстремальной точки).

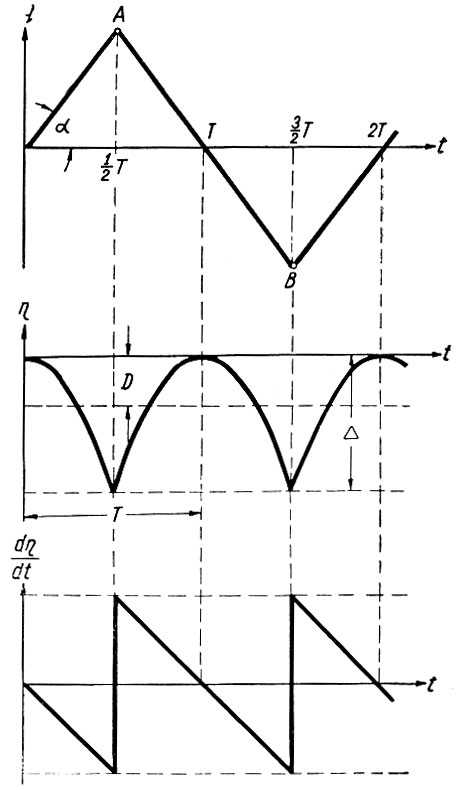
Рис. 6.24. Характеристики экстремального управления

В соответствии с этим (ур. 6.3) η также осуществляет рыскание, но (рис. 6.24) с вдвое меньшим периодом. Этот период (Т) получил название периода рыскания. Максимальное отклонение параметра η от его экстремального значения называется амплитудой рыскания выхода и обозначается (рис. 6.24) буквой Δ.

Как следует из рис. 6.24, входной параметр (q) на участке 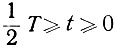изменяется в соответствии со следующим законом:

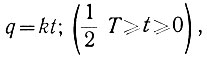(6.4)

где k = tg α - коэффициент, определяющий наклон характеристики q = φ(t) относительно оси абсцисс.

Подставив в уравнение (6.3) значение q, получаем

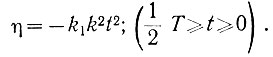(6.5)

Поэтому скорость изменения экстремального параметра на участке 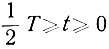определяется зависимостью

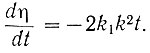(6.6)

Эта характеристика показана на нижнем графике рис. 6.24. В момент 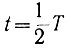происходит реверс системы и производная экстремального параметра меняет свой знак. Дальнейший характер изменения производной виден из рис. 6.24. Максимальное значение этой производной, при которой происходит реверс системы, называется критической величиной.

Среднее за период рыскания значение (D) экстремального параметра называется потерей на рыскание и определяется следующим образом:

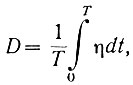
где Т - период рыскания системы.

Подставив в это уравнение значение η (ур. 6.5) и изменив пределы интегрирования, получаем

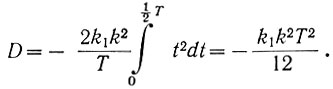(6.7)

Следует иметь в виду, что поскольку потеря на рыскание является интегральной величиной, то она равна постоянной составляющей экстремального параметра (η), ибо среднее за период рыскания значение всех гармонических составляющих равно нулю.

Амплитуда рыскания (рис. 6.24) определяется уравнением (6.5), если в него подставить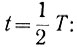

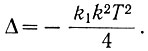(6.8)

Сравнивая уравнения (6.7) и (6.8), легко увидеть, что амплитуда рыскания в три раза больше величины потери на рыскание:

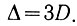(6.9)

Как следует из рис. 6.24, критическая величина производной экстремального параметра (ур. 6.6) равна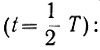

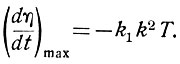(6.10)

Решая совместно уравнения (6.7) и (6.10), получаем

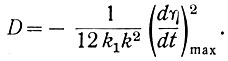
Следовательно, для уменьшения потери на рыскание необходимо уменьшать критическое значение производной. Однако это уменьшение ограничивается возможностью появления ошибочных реверсов системы.

Период рыскания также необходимо выбирать как можно меньшим, так как это сокращает время выхода системы в область экстремальной точки. При этом необходимо только иметь в виду, что при малых значениях периода возникают трудности различения изменений входной величины (q), связанных с рысканием системы, и изменений, обусловленных случайными процессами (например, высокочастотными помехами).