
11. Динамика выхода самонастраивающейся системы в область экстремума
Рассмотрим динамику выхода самонастраивающейся системы в область экстремума после ее включения.
Пусть входная линейная часть (рис. 6.25) является интегрирующим звеном, т. е. сигнал q непрерывно растет при положительном (ур. 6.11.) значении напряжения u1 и уменьшается - при отрицательной величине u1. Следовательно, для входной части (ур. 6.4) можно записать, что
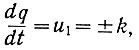 (6.12)
(6.12)где k - постоянная величина.
Выходная линейная часть системы, как уже отмечалось ранее, описывается дифференциальным уравнением первого порядка. Поэтому его передаточная функция имеет следующий вид:
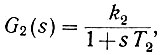 (6.13)
(6.13)где Т2 - постоянная времени выходной части;
k2 - коэффициент усиления этой части.
Следовательно, соотношение между лапласовыми изображениями напряжений на выходе и входе выходной линейной части равно
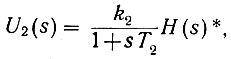
где Н(s) - лапласово изображение функции η(t).
* (Здесь, как и ранее, лапласовы изображения [U2(s) и H(s)] в отличие от исходных функций [u2(t) и η(t)] обозначаются большими буквами.)
Запишем это уравнение в несколько ином виде:
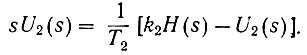
Тогда, переходя от изображений Лапласа к исходным функциям, получаем
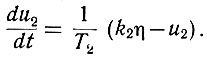 (6.14)
(6.14)Примем далее, что реверс системы осуществляется искателем экстремума в тот момент, когда величина отклонения напряжения u2 (на выходе системы) достигнет величины
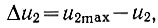 (6.15)
(6.15)где u2mах - экстремальное значение напряжения на выходе системы;
Δu2 - заданная величина отклонения напряжения от экстремального значения.
Решая совместно уравнения (6.12) и (6.14), получаем
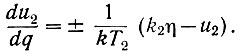 (6.16)
(6.16)Как следует из этого уравнения, максимальное значение напряжения (u2) на выходе системы достигается при условии
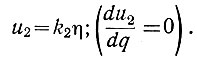 (6.17)
(6.17)Если же соответственно изменить масштаб экстремального параметра (ввести ηм = k2η), то напряжение u2 будет иметь максимальное значение при
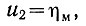 (6.17а)
(6.17а)т. е. в точках пересечения кривых u2 = φ(q) и ηм = f(q).
Основываясь на этом, рассмотрим динамику выхода системы в область экстремума.
Допустим (рис. 6.28), что система находится в начале координат (точка а). При увеличении q в окрестности точки а из-за наличия запаздывания в выходной части системы будет иметь место неравенство
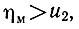 (6.18)
(6.18)т. е. кривая u2 = φ(q) пойдет ниже кривой ηм = f(q).
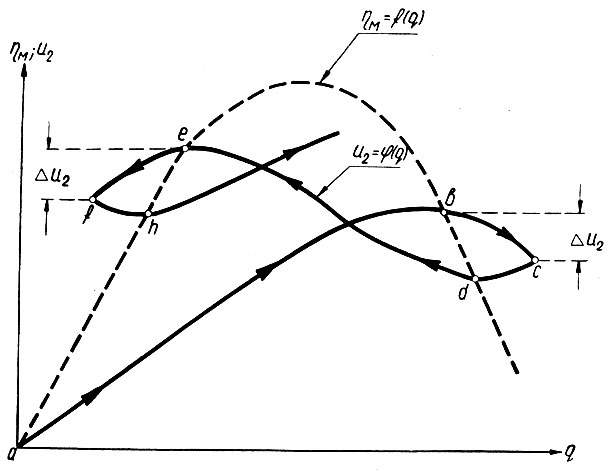
Рис. 6.28. Динамика выхода системы в область экстремума
Поскольку при этом q возрастает, то (ур. 6.16 и 6.18) в окресностях точки а
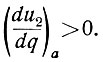
Так будет продолжаться до точки b, в которой кривые u2 = φ(q) и ηм = f(q) пересекаются. Поэтому (ур. 6.17а) в точке b
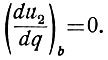
После достижения в точке b максимума напряжение u2 начинает уменьшаться. Как только (ур. 6.15) разница u2b - u2 достигнет величины Δu2, произойдет реверс системы (точка с). В этот момент напряжение на входе системы (u1) меняет знак на обратный и (ур. 6.11) становится равным
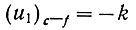
и q начинает уменьшаться.
После точки с кривая u2 = φ(q) вначале идет выше кривой ηм = f(q). Поэтому (u2 > ηм), учитывая то что перед правой частью уравнения (6.16) стоит знак минус (u1 = -k), получим
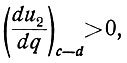
т. е. кривая u2 = φ(q) имеет положительную кривизну.
Поскольку после точки с параметр q уменьшается, а функция u2 = f(q) имеет положительную кривизну, то напряжение u2 также уменьшается. Поэтому в определенной точке (d) кривые u2 = φ(q) и ηм = f(q) пересекаются. Так как в точке d наступает равенство u2 = ηм = k2η, то производная в этой точке равна (ур. 6.16)
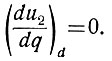
После точки d напряжение u2 становится меньше ηм; поэтому (ур. 6.16) кривая u2 = φ(q) опять имеет отрицательную кривизну (ибо u1 = -k):
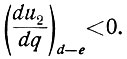
Легко увидеть, что в точке е эта производная вновь становится равной нулю. После точки е напряжение u2 начинает снижаться, так как q продолжает уменьшаться, а производная (u2 > ηм) становится больше нуля:
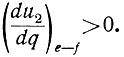
В точке f разница u2е - u2 достигает Δu2, и система вновь реверсируется, благодаря чему q начинает возрастать.
Так будет продолжаться до тех пор, пока система не выйдет в область экстремума и не начнет совершать колебания (рыскания) возле экстремальной точки.
Кривая u2 = φ(q), характеризующая установившийся режим рыскания, называется предельным циклом рыскания (рис. 6.29). Характерной особенностью предельного цикла, отличающего его от динамических циклов выхода системы в область экстремума (рис. 6.28), является условие попадания любой точки цикла (например, точки A, рис. 6.29) самой в себя после завершения двух периодов рыскания (для точки A: от A до B и обратно).
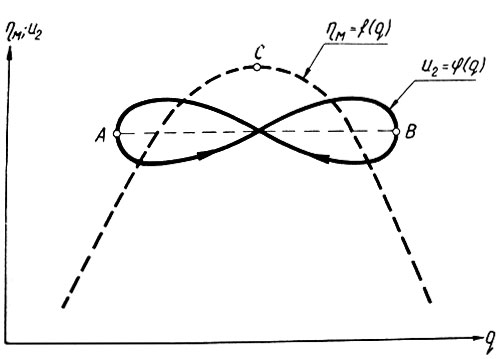
Рис. 6.29. Предельный цикл рыскания
Система работает в предельном цикле до тех пор, пока не произойдет смещение экстремальной точки (С). После смещения этой точки система начинает двигаться в область нового экстремума, пока не выйдет на новый предельный цикл.
Рассмотрим теперь математическое описание динамики выхода системы в область экстремума (рис. 6.28) и работы ее в предельном цикле (рис. 6.29). При этом для упрощения изложения примем, что экстремальная характеристика η = f(q) является параболой. Методом, аналогичным описываемому ниже, можно проследить выход системы в область экстремума и при любом другом виде экстремальной характеристики.
Как следует из рис. 6.28, динамическая кривая выхода самонастраивающейся системы [u2 = φ(q)] состоит из ряда полуциклов рыскания. В положительном полуцикле параметр q увеличивается. Затем положительный полуцикл сменяется отрицательным, при котором q уменьшается. Выполнив ряд полуциклов, система выходит в область экстремума и начинает работать в предельных полуциклах рыскания (рис. 6.29).
Таким образом, для того чтобы описать поведение системы, достаточно найти уравнение системы для положительного и отрицательного полуциклов.
Рассмотрим вначале положительный полуцикл, начинающийся в произвольно заданной точке с координатами u2 и q0.
Поскольку в положительном полуцикле (ур. 6.11) напряжение (u1) на входе системы (рис. 6.25) равно +k, то, подставив значение η (ур. 6.3) в уравнение (6.16), получим
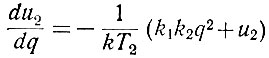
или
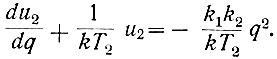 (6.19)
(6.19)Решив это уравнение, можно определить искомую зависимость.
Ранее было сказано, что это уравнение (полуцикл) имеет ненулевые начальные условия (u2 и q0). Поэтому для того чтобы эти условия стали нулевыми, введем новые переменные
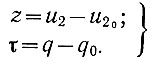 (6.20)
(6.20)Тогда dz = du2, dτ = dq. Поэтому
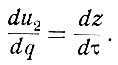 (6.20а)
(6.20а)
Подставив значения u2, q (ур. 6.20) и 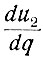 (ур. 6.20а) в уравнение (6.19), получаем
(ур. 6.20а) в уравнение (6.19), получаем
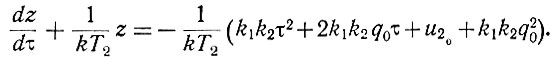 (6.21)
(6.21)Эта зависимость отличается от уравнения (6.19) тем, что она уже имеет нулевые начальные условия. Действительно, как следует из условий (6.20), при q = q0 переменная τ = 0. Вместе с тем, при q = q0 напряжение u2 = u20. Поэтому (ур. 6.20) в данном случае z = 0.
Поскольку уравнение (6.21) имеет нулевые начальные условия, то, переходя от переменных z и τ к изображениям Лапласа, записываем
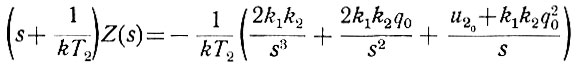
или
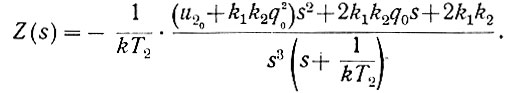
Раскладывая правую часть этого уравнения на простейшие дроби, получаем
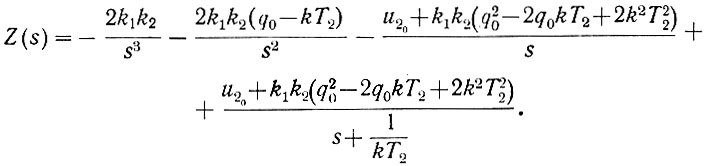
Пользуясь таблицами преобразованных функций, находим исходную функцию
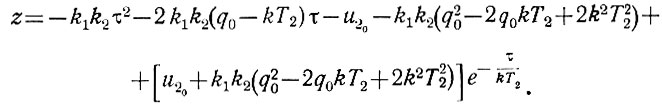
Подставив в это выражение значения z и τ (ур. 6.20), после несложных преобразований получаем
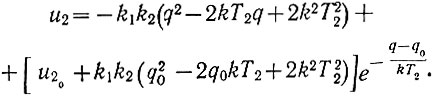 (6.22)
(6.22)Полученная зависимость является уравнением положительного полуцикла движения системы, происходящего при возрастании параметра q. Для того чтобы получить уравнение отрицательного полуцикла, достаточно в уравнении (6.19), а следовательно, и в уравнении (6.22) изменить знак перед коэффициентом k, ибо в отрицательном полуцикле (ур. 6.11) u1 = -k.
Поэтому (ур. 6.22) для отрицательного полуцикла можно записать
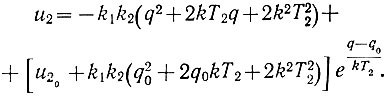 (6.23)
(6.23)Построение всей кривой, характеризующей динамику выхода системы в область экстремума, выполняется следующим образом.
Перенесем, как это уже делалось ранее, начало координат в экстремальную точку (рис. 6.23). Тогда в начале работы системы параметры u2 и q0 будут равны не нулю, как на рис. 6.28, а, соответственно, u2а и qa (рис. 6.30).
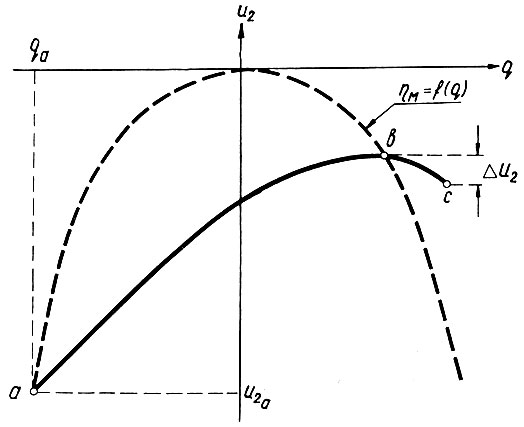
Рис. 6.30. Характеристики системы при переносе начала координат в экстремальную точку
Поэтому, подставив в уравнение (6.22) значения u20 = u2a и q0 = qa, получим уравнение первого положительного полуцикла движения системы
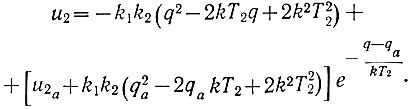 (6.24)
(6.24)Построим эту кривую (рис. 6.30). Вначале напряжение будет возрастать, но в точке b его рост прекратится и начнется уменьшение. В тот момент, когда напряжение u2 станет равным u2с:
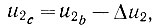 (6.25)
(6.25)произойдет реверс системы. Поэтому в точке c начнет свое начало первый отрицательный полуцикл рыскания системы.
Координаты точки c определяются следующим образом. В точке b кривые ηм = f(q) u2 = φ(q) пересекаются (u2b = ηмb). Поэтому, приравняв при q = qb правые части уравнения (6.24) и зависимости ηм = -k1k2q2 (ур. 6.3 и замечание выше), получаем следующую характеристику:
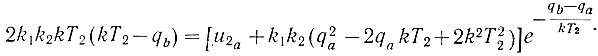 (6.26)
(6.26)Это уравнение позволяет определить величину qb.
Зная qb, из уравнения (6.24) можно определить вторую координату точки b - напряжение u2b. Затем, поскольку Δu2 задано, уравнение (6.25) дает возможность найти u2с. Зная u2с, можно (ур. 6.24) найти и qc.
Подставив в уравнение (6.23) начальные значения параметров q0 = qc и u20 = u2c, получим уравнение первого отрицательного полуцикла.
Продолжив это построение, можно получить всю динамическую кривую, показывающую выход системы в область экстремума.
Пример. Пусть нам задана экстремальная характеристика системы
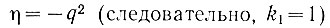
и координаты ее начальной точки: u2а = -9в; qa = -3в. Кроме того, дано: k = 1; k2 = 1; Т2 = 2 сек; Δu2 = 0,25в.
Подставляя эти данные в уравнение (6.24), определяем характеристику первого положительного полуцикла:
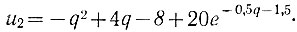 (6.27)
(6.27)Находим далее координату qb. Подставив значения параметров в уравнение (6.26), получаем:
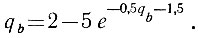
Решая (методом подбора) это уравнение относительно qb, получаем
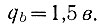
Подставляя значение qb в уравнение (6.27), определяем напряжение в точке b:
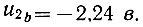
Далее определяем координаты точки c. Подставляя в уравнение (6.25) значения u2b и Δu2, подсчитываем первую координату:
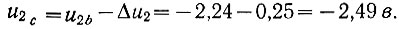
Как следует из уравнения (6.27), в этой точке (u2с = -2,49в)
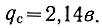
Точка c с координатами qc = 2,12в и u2с = -2,49в является начальной для первого отрицательного полуцикла движения. Поэтому, подставив в уравнение (6.23) заданные значения параметров и учитывая, что q0 = qc = 2,14в, a u20 = u2с = -2,49в, получаем уравнение первого отрицательного полуцикла движения:
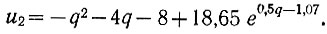
Далее можно, как и для первого положительного полуцикла, найти последнюю точку для первого отрицательного полуцикла. Эта точка будет начальной для второго положительного полуцикла... Продолжая это решение, можно построить всю динамическую кривую выхода системы в область экстремума.
Уравнения (6.22) и (6.23) определяют любые полуциклы движения системы, в том числе и предельные.
Положительный полуцикл станет предельным в том случае, если он проходит через точки А, В и С (рис. 6.31). Причем точки А и С имеют равные ординаты (u2A = u2C) и одинаково удалены от оси ординат (qA = -qC). В точке В кривые ηм = f(q) и u2 = φ(q) пересекаются. Эти условия позволяют определить уравнения предельных полуциклов.
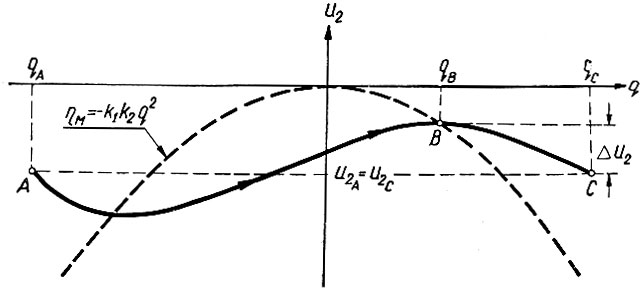
Рис. 6.31. Параметры предельного полуцикла
Для положительного предельного полуцикла (рис. 6.31) начальной является точка А. Поэтому, подставив в уравнение (6.22) начальные условия u20 = u2A и q0 = qA, получим характеристику положительного предельного полуцикла:
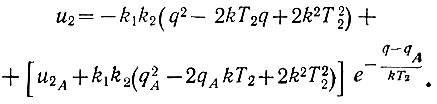 (6.28)
(6.28)В этом уравнении имеются два неизвестных параметра - координаты точки А (u2A и qA). Найдем дополнительные условия, которые позволят определить эти параметры.
Ранее говорилось о том, что кривая предельного положительного полуцикла проходит через точку С. Поэтому, подставив в уравнение (6.28) q = qC, получаем
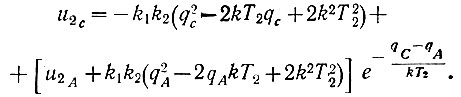 (6.29)
(6.29)В точке В (рис. 6.31) кривые ηм = f(q) и u2 = φ(q) пересекаются. Поэтому для этой точки (ур. 6.3 и 6.17) можно записать:
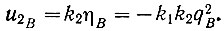 (6.30)
(6.30)Поскольку (ур. 6.25)
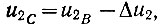
то, учитывая уравнение (6.30), получаем
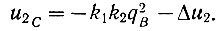 (6.31)
(6.31)Кроме того, подставляя в уравнение (6.28) q = qB, записываем
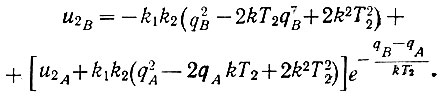
Подставляя в это уравнение значения u2В (ур. 6.30) и qB (ур. 6.31), получаем
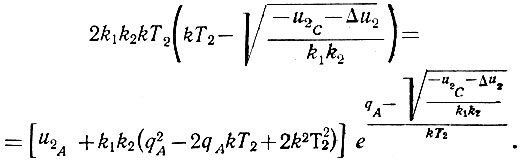
Как уже указывалось ранее, предельный полуцикл отличается от других полуциклов тем, что координаты точек его начала (А) и конца (С) связаны следующими зависимостями:
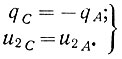 (6.33)
(6.33)Поэтому, подставив данные условия в уравнения (6.29) и (6.32), получаем
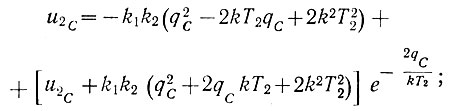 (6.34)
(6.34)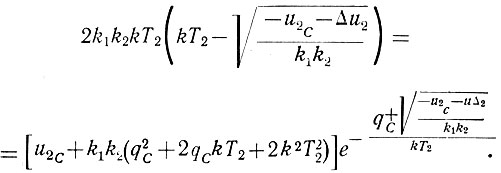 (6.35)
(6.35)Решая совместно эти уравнения, можно найти координаты точки С (qC и u2C). Тем самым (ур. 6.33) будут определены и координаты точки А. После этого по уравнению (6.28) можно построить кривую положительного предельного полуцикла рыскания. Если же в уравнении (6.28) изменить знак перед k и вместо qA и u2А записать новые начальные условия (qC и u2С), то можно определить характеристику отрицательного предельного полуцикла рыскания:
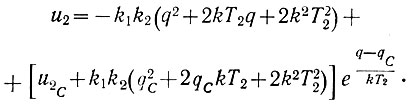 (6.36)
(6.36)Пример определения характеристики предельного полуцикла. Возьмем те же параметры, что и в предыдущем примере: k = 1; k1 = 1; k2 = 1; T2 = 2 сек; Δu2 = 0,25 в.
Подставим эти данные в уравнения (6.34) и (6.35):
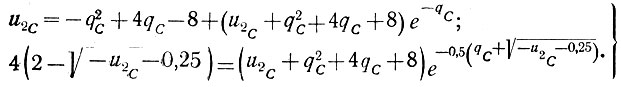 (6.37)
(6.37)Решая методом подбора данные уравнения, получаем:
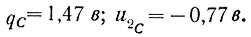
Следовательно (ур. 6.33), координаты точки А равны:
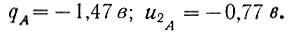
Подставив в уравнение (6.28) заданные в примере значения параметров k, k1, k2 и T2, а также начальные условия (qA и u2A), получаем характеристику положительного предельного полуцикла рыскания:
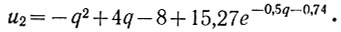
Аналогично, подставив полученные данные в уравнение (6.36), определяем характеристику отрицательного предельного полуцикла рыскания:
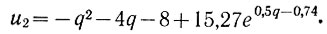
Рассмотрим далее, как изменяется во времени напряжение на выходе системы (рис. 6.25) при работе ее в предельных циклах рыскания.
Предположим, как это делалось и ранее, что скорость изменения параметра q всегда (по величине) остается постоянной. Тогда для предельного цикла рыскания (рис. 6.31) q будет изменяться в соответствии с графиком, показанным на рис. 6.32. В соответствии с этим графиком в течение первого периода рыскания Т (положительного полуцикла) параметр q имеет следующую зависимость от времени:
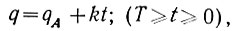 (6.38)
(6.38)где k = tg α.
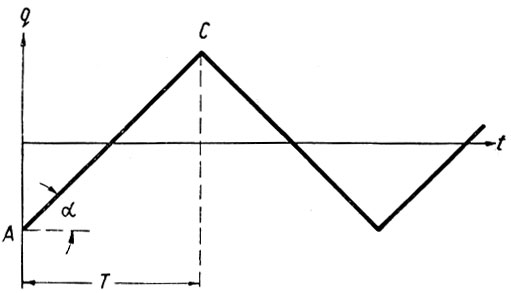
Рис. 6.32. Характеристика параметра q
Подставив значение q в характеристику положительного предельного полуцикла (ур. 6.28), получим:
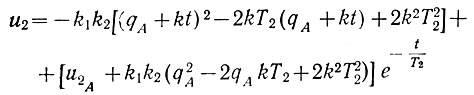
или после несложных преобразований будем иметь:
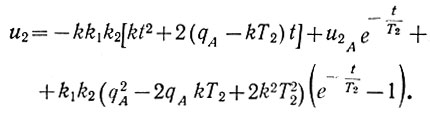 (6.39)
(6.39)Проследить за изменением экстремального параметра η во времени можно, подставив в уравнение (6.3) значение q (ур. 6.38). В результате получим
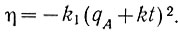 (6.40)
(6.40)Как было показано в разделе 6.9, потеря на рыскание (D) определяется как среднее за период рыскания значение экстремального параметра:
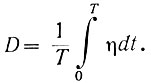 (6.41)
(6.41)Прежде всего необходимо определить период рыскания (Т). Как следует из рис. 6.31 и 6.32, период рыскания системы равен времени ее движения из точки А в точку С (или обратно). Поэтому, приравняв (ур. 6.38) q = qC, получаем
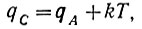
откуда
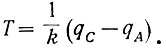
Подставив в это выражение qC (ур. 6.33), определяем период рыскания:
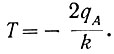 (6.42)
(6.42)Теперь подставим в уравнение (6.41) значение η (ур. 6.40) и Т (ур. 6.42). Тогда получаем
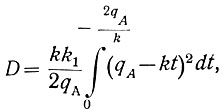
откуда после интегрирования определяем потерю на рыскание:
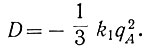 (6.43)
(6.43)Для рассмотренного выше примера потеря на рыскание составляет
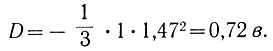

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
