12. Устойчивость работы самонастраивающейся системы

Ранее было введено ограничение, согласно которому быстродействие работы системы во много раз превышает скорость ухода (дрейфа) экстремальной точки вследствие изменения во времени экстремальной характеристики η = f(q).

Поэтому при отсутствии в системе элементов, содержащих индуктивность и емкость, она всегда является устойчивой. Однако в том случае, когда в системе имеются инерционные элементы, устойчивость работы системы может быть нарушена и она не выйдет в область экстремума.

Рассмотрим этот вопрос на примере шаговой системы, в которой через равные промежутки времени (Δt) измеряется величина экстремального параметра (η) и при

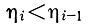
осуществляется реверс системы.

Для упрощения будем считать, что при определении необходимости реверса сравниваются не средние (на участках Δt) значения η, а мгновенные величины, измеряемые через каждые Δt сек. Кроме того, примем, что искатель экстремума не имеет зоны нечувствительности.

Поэтому в отличие от рис. 6.18 (верхний график) в левой части рис. 6.33 разместим непрерывную кривую η = f(q). Предположим также, что в изучаемой системе нет выходной линейной части, т. е. что запаздывание на выходе системы отсутствует.

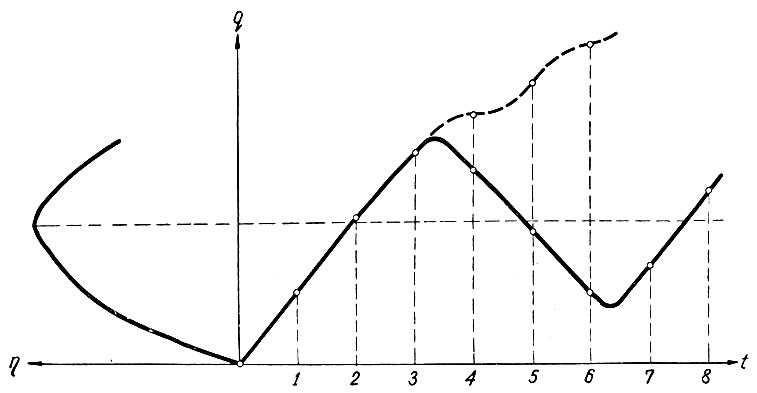
Рис. 6.33. Характеристика устойчивой и неустойчивой систем

Рассмотрение начнем с начального момента (рис. 6.33), когда q = 0. В этот момент напряжение на входе (u₁) системы (рис. 6.25) равно +k, и в соответствии с этим q начинает возрастать. В точках 1 и 2 неравенство η_i < η_i-1 отсутствует. Наконец, в точке 3 появилось неравенство η_i < η_i-1 и в системе происходит реверс напряжения u₁. Поскольку в системе имеется входная линейная часть, вносящая запаздывание, то дальше возможны два случая работы системы.

а) Запаздывание на входе системы очень мало

В этом случае (рис. 6.33) после точки 3 параметр q еще несколько возрастает, а затем начинается его относительно быстрое уменьшение. В соответствии с уменьшением q экстремальный параметр растет. Поэтому в точке очередного замера (в точке 4) окажется, что η_i > η_i-1 и система будет продолжать двигаться к экстремальной точке. Следовательно, несмотря на наличие запаздывания, система осуществляет обычное рыскание в области экстремума.

б) Запаздывание на входе относительно велико

Если запаздывание велико, то может случиться, что после того как в точке 3 произошел реверс напряжения u₁, параметр q из-за инерционности входной линейной части (рис. 6.25) будет еще продолжать возрастать.

Тогда в очередной момент проверки (в точке 4) окажется, что η_i < η_i-1, и в системе опять будет дан сигнал на реверс, но на этот раз - в неправильную сторону, ибо после этого реверса система будет стремиться увеличивать q, в то время как этот параметр должен уменьшаться. Поэтому система, совершая колебательные движения, начнет уходить из области экстремума (прерывистая кривая на рис. 6.33) и устойчивость работы системы будет нарушена.

В том случае, когда запаздывание имеется как на входе, так и на выходе системы, ее устойчивость лучше рассматривать на основе изучения поведения кривой u₂ = φ(q).

В устойчивой системе (рис. 6.34) после реверса (точка 3) q еще несколько возрастает, но затем начинает уменьшаться (точка 4^а). В неустойчивой системе (прерывистая кривая) q после точки 3 продолжает возрастать, совершая при этом колебательные движения.

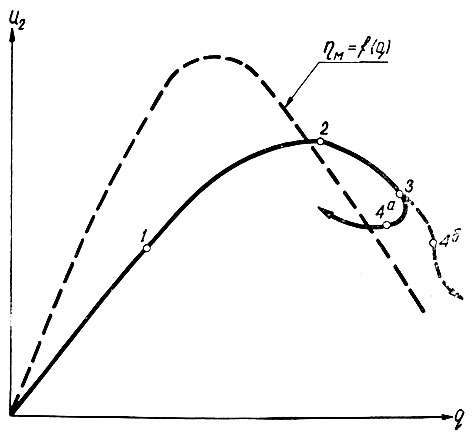
Рис. 6.34. Динамические характеристики системы

Таким образом, исследуя характеристику u₂ = φ(q), можно определить устойчивость самонастраивающейся системы и проследить за динамикой ее выхода в область экстремума.